网络流学习笔记

这是信息学中比较重要的一个算法了，可以用来处理很多图论模型。

先说说网络最大流，主要来自进阶指南，blog的学习。

非常重要的增广路定理回家看算导吧qwq

首先介绍一些基本的网络流的概念。

什么是网络流

在一个有向图上选择一个源点，一个汇点，每一条边上都有一个流量上限（以下称为容量），即经过这条边的流量不能超过这个上界，同时，除源点和汇点外，所有点的入流和出流都相等，而源点只有流出的流，汇点只有汇入的流。这样的图叫做网络流。

所谓网络或容量网络指的是一个连通的赋权有向图 D= （V、E、C），其中V 是该图的顶点集，E是有向边(即弧)集，C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流，这是定义在网络上的非负函数，它一方面受到容量的限制，另一方面除去起点和终点以外，在所有中途点要求保持流入量和流出量是平衡的。（引自百度百科）

定义

我们定义：
源点：只有流出去的点
汇点：只有流进来的点
流量：一条边上流过的流量
容量：一条边上可供流过的最大流量
残量：一条边上的容量-流量

几个基本性质

基本性质一：

对于任何一条流，总有流量<=容量

这是很显然的

基本性质二

对于任何一个不是源点或汇点的点u，总有

$\sum_{p∈E}k[p][u]=\sum_{q∈E}k[u][q]$（其中k[i][j]表示i到j的流量

这个也很显然，即一个点（除源点和汇点）的入流和出流相等

基本性质三

对于任何一条有向边(u,v)，总有

$k[u][v]==−k[v][u]$

这个看起来并不是很好理解，它的意思就是一条边的反边上的流是这条边的流的相反数，可以这么想，就是如果有k[u][v]的流从u流向v，也就相当于有-k[v][u]的流从v流向u。这条性质非常重要。

这些都不是很难理解，不过对于性质三，他有什么用呢？

后面关于巧妙调整网络中的流量就知道了。

既然是图论，接下来肯定少不了图。

~~抄袭严重~~

面是所有最大流算法的精华部分：引入反向边为什么要有反向边呢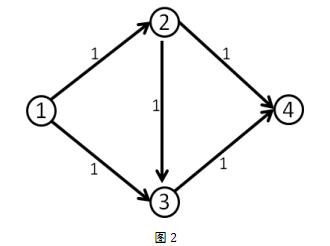？ ek1 我们第一次找到了1-2-3-4这条增广路，这条路上的delta值显然是1。于是我们修改后得到了下面这个流。（图中的数字是容量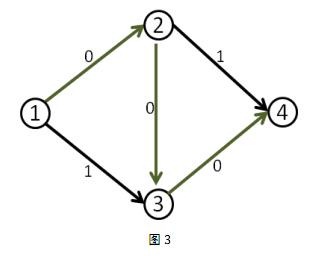） ek2 这时候(1,2)和(3,4)边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但这个答案明显不是最大流，因为我们可以同时走1-2-4和1-3-4，这样可以得到流量为2的流。

那么我们刚刚的算法问题在哪里呢？问题就在于我们没有给程序一个”后悔”的机会，应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢？回溯搜索吗？那么我们的效率就上升到指数级了。

而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i)，反向边也同样有它的容量。

我们直接来看它是如何解决的：

在第一次找到增广路之后，在把路上每一段的容量减少delta的同时，也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时，inc(c[y,x],delta)

我们来看刚才的例子，在找到1-2-3-4这条增广路之后，把容量修改成如下

ek3

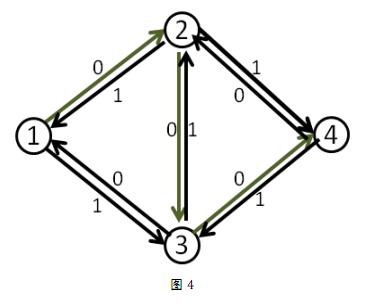
这时再找增广路的时候，就会找到1-3-2-4这条可增广量，即delta值为1的可增广路。将这条路增广之后，得到了最大流2。

ek4

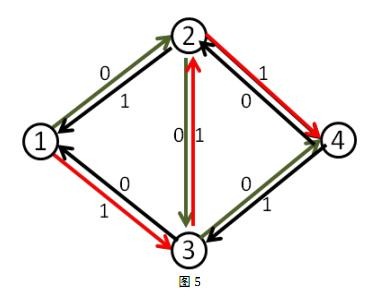
那么，这么做为什么会是对的呢？我来通俗的解释一下吧。

事实上，当我们第二次的增广路走3-2这条反向边的时候，就相当于把2-3这条正向边已经是用了的流量给”退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。（有人问如果这里没有2-4怎么办，这时假如没有2-4这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点）同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流量。

这就是这个算法的精华部分，利用反向边，使程序有了一个后悔和改正的机会

换句话说我们用巧妙的方式配合增广路定理避免了搜索回溯来寻找最优方案。

由于状态不好，只写出来了EK（居然跑过了1e4点1e5边的图，luogu数据是真的水）

Code：

// luogu-judger-enable-o2
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <queue>
#include <cstring>
#define maxn 10005
#define maxm 100005
#define INF 0x7ffffff
int head[maxn] , ct = 1 , n , m , s , t , MaxFlow, fw[maxn] , pre[maxn] , Epre[maxn];
struct edge{
    int nxt , to , dis;
}e[maxm<<1];

inline void add(int x , int y , int d)
{
    e[++ct] = (edge){head[x],y,d};
    head[x] = ct;
}

inline int bfs(int s , int t)
{
    std::memset(pre,-1,sizeof(pre));
    std::memset(Epre,-1,sizeof(Epre));
    pre[s] = Epre[s] = 0;
    std::queue<int> q;
    q.push(s);
    fw[s] = INF;
    for( ; q.size() ; q.pop())
    {
    int nw = q.front();
    if(nw == t) break;
    for(int i = head[nw] ; i ; i = e[i].nxt)
        if(e[i].dis > 0 && !~pre[e[i].to]) fw[e[i].to] = std::min(fw[nw] , e[i].dis) , Epre[e[i].to] = i , pre[e[i].to] = nw , q.push(e[i].to);
    }
    if(~pre[t]) return fw[t];
    else return -1;
}

inline void EK(int s , int t)
{
    int flow = 0;
    while(~(flow = bfs(s,t)))
    {
//	printf("Cur Arguement Way:%d\n",flow);
    int k = t;
//	printf("THE ROAD\n");
    while(k != s)
    {
//	    printf("%d ",k);
        e[Epre[k]].dis -= flow;
        e[Epre[k]^1].dis += flow;
        k = pre[k];
    }
//	printf("THE FLOW: %d\n",flow);
    MaxFlow += flow;
    }
}

int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i = 1 ; i <= m ; ++i)
    {
    int x , y , d;
    scanf("%d%d%d",&x,&y,&d);
    add(x,y,d) , add(y,x,0);
    }
    EK(s,t);
    printf("%d",MaxFlow);
}