Post 32

Veröffentlicht am | Edited on

无论如何困难，不可求人怜悯。

LOJ #6278. 数列分块入门 2

题目描述

给出一个长为 nn 的数列，以及 nn 个操作，操作涉及区间加法，询问区间内小于某个值 xx 的元素个数。

输入格式

第一行输入一个数字 nn。

第二行输入 nn 个数字，第 ii 个数字为 a_iai，以空格隔开。

接下来输入 nn 行询问，每行输入四个数字 \mathrm{opt}opt、ll、rr、cc，以空格隔开。

若 \mathrm{opt} = 0opt=0，表示将位于 [l, r][l,r] 的之间的数字都加 cc。

若 \mathrm{opt} = 1opt=1，表示询问 [l, r][l,r] 中，小于 c^2c2 的数字的个数。

输出格式

对于每次询问，输出一行一个数字表示答案。

样例

样例输入

1
2
3
4
5
6
4
1 2 2 3
0 1 3 1
1 1 3 2
1 1 4 1
1 2 3 2

样例输出

1
2
3
3
0
2

数据范围与提示

对于 100\%100% 的数据，$1 \leq n \leq 50000,$

题解

想了半个小时才想出来怎么做，vector果然是好东西。

我们还是对序列分块，不过先想一想假如给你一个序列让你多次查找小于某个值的数个数有多少个，会怎么做？

排序+二分。

想到这里就不难构思出做法了。

对每个块用一个vector维护，块内元素是值和下标（下标是为了在块值有序的情况下完成不完整块的修改）对于每次修改，完整的块打懒标记即可，不完整的的块暴力遍历下标在修改区间内的元素，将值修改后对块排序。

查询时对于不完整的块暴力遍历，对于其下标在区间里的元素判断是否符合条件并统计答案。完整的块可以二分查找统计答案。

设块大小为$S$

这样做，修改时间复杂度是$O(n/S+2SlogS)$

查询的复杂度是$O(n/Slogn+2S)$

这个东西显然有比$\sqrt{n}$更优的值，就不讨论了。

值得一说的是本来思路清晰写上去感觉能一遍过的，结果全WA了，然后我又是2节课各种分析数据，定位错误位置，最终得出结论：同块查询有误。

然后我又20分钟整个数据生成器，拍了个极小数据居然错了。。

然后我一看，惊喜的发现：

img

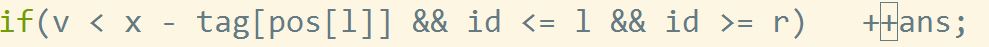
以后检查不要放过任何一个语句。。。哪怕是最显然的。

不过感觉最高效的做法还是争取写的时候一遍写对，不然这种调试太。。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#define maxn 50005
#define maxsqrt 235
struct Node{
	int v , id;
	bool operator < (const Node& x)const{
		return v < x.v;
	}
};
std::vector<Node> bl[maxsqrt];
int blsize , blnum ,  n , tag[maxsqrt] , L[maxsqrt] , R[maxsqrt] , pos[maxn] , a[maxn] , _de;

inline void pre()
{
	blsize = (int)std::pow(n,0.5);
	blnum = n / blsize;
	for(int i = 1 ; i <= blnum ; ++i)
		L[i] = (i-1)*blsize+1 , R[i] = i*blsize;
	if(R[blnum] < n) ++blnum , L[blnum] = R[blnum-1] + 1 , R[blnum] = n;
	for(int i = 1 ; i <= blnum ; ++i)
		for(int j = L[i] ; j <= R[i] ; ++j)
			pos[j] = i;
	for(int i = 1 ; i <= n ; ++i)
		bl[pos[i]].push_back((Node){a[i],i});
	for(int i = 1 ; i <= blnum ; ++i)
		std::sort(bl[i].begin(),bl[i].end());
}

inline void update(int l , int r , int v)
{
	if(pos[l] == pos[r]) //in the same block
	{
		for(int i = 0 ; i < (int)bl[pos[l]].size() ;++i)
			if(bl[pos[l]][i].id <= r && bl[pos[l]][i].id >= l)
				bl[pos[l]][i].v += v;
		std::sort(bl[pos[l]].begin(),bl[pos[l]].end());
		return;
	}

	int nl , nr;
	if(L[pos[l]] == l) nl = l;
	else nl = L[pos[l]+1];
	if(R[pos[r]] == r) nr = r;
	else nr = R[pos[r]-1];
	
	int pl = pos[l] , pr = pos[r];
	for(int i = 0 ; i < (int)bl[pl].size() ; ++i)
		if(bl[pl][i].id >= l && bl[pl][i].id < nl)
			bl[pl][i].v += v;
	std::sort(bl[pl].begin() , bl[pl].end());
	for(int i = 0 ; i < (int)bl[pr].size() ; ++i)
		if(bl[pr][i].id <= r && bl[pr][i].id > nr)
			bl[pr][i].v += v;
	std::sort(bl[pr].begin() , bl[pr].end());

	if(nl > nr) return; // adjancent block update

	for(int i = pos[nl] ; i <= pos[nr] ; ++i)
		tag[i] += v;
	return ;
}


inline int find(std::vector<Node>& v , int key)
{
	int l = 0 , r = v.size() - 1 , ans = -1;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(v[mid].v < key) ans = mid , l = mid + 1;
		else r = mid - 1;
	}
	return ans;
}

inline void print()
{
	puts("NOW THE ARRAY");
	int tmp[maxn];
	for(int i = 1 ; i <= blnum ; ++i)
	{
		for(int j = 0 ; j < (int)bl[i].size() ; ++j)
			tmp[bl[i][j].id] = bl[i][j].v;
		for(int j = L[i] ; j <= R[i] ; ++j)
			printf("%d ",tmp[j] + tag[i]);
	}
	putchar(10);
}

inline int query(int l , int r , int x)
{
//	printf("QUERY!!!!!%d %d %d\n",l,r,x);
	int ans = 0;
//	printf("THE BLOCK%d %d\n",pos[l],pos[r]);
	if(pos[l] == pos[r])
	{
		for(int i = 0 ; i < (int)bl[pos[l]].size() ; ++i)
		{
			int v = bl[pos[l]][i].v , id = bl[pos[l]][i].id;
	//		printf("(%d , %d) ",v,id);
	//		printf("SHIT!%d < %d - %d && %d <= %d && %d >= %d?",v,x,tag[pos[l]],id,l,id,r);
			if(v < x - tag[pos[l]] && id >= l && id <= r)	++ans;
		}
		return ans;
	}

	int nl , nr;
	if(L[pos[l]] == l) nl = l;
	else nl = L[pos[l]+1];
	if(R[pos[r]] == r) nr = r;
	else nr = R[pos[r]-1];
	
	int pl = pos[l] , pr = pos[r];
	for(int i = 0 ; i < (int)bl[pl].size() ; ++i)
		if(bl[pl][i].id < nl && bl[pl][i].id >= l && bl[pl][i].v < x - tag[pl])
			++ans;
	for(int i = 0 ; i < (int)bl[pr].size() ; ++i)
		if(bl[pr][i].id > nr && bl[pr][i].id <= r && bl[pr][i].v < x - tag[pr])
			++ans;
//	printf("THE IMCOMPLETE BLOCK ANS: %d\n",ans);
//	printf("THE CBLOCK %d %d\n",nl,nr);

	if(nl > nr) return ans;

	for(int i = pos[nl] ; i <= pos[nr] ; ++i)
		ans += find(bl[i] , x-tag[i]) + 1;
//	printf("THE TOTAL BLOCK ANS: %d\n",ans);
	return ans;

}

int main()
{
//	freopen("data.in","r",stdin);
//	freopen("my.out","w",stdout);
	scanf("%d",&n);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&a[i]);
	pre();
	for(int i = 1 ; i <= n ; ++i)
	{
		int op , l , r , x;
		scanf("%d%d%d%d",&op,&l,&r,&x);
		if(op == 1)
			printf("%d\n",query(l,r,x*x));
		else update(l,r,x);
//		printf("THE ith operation:%d\n",i);
//		print();
	}
}

LOJ #6279. 数列分块入门 3

题目描述

给出一个长为 nn 的数列，以及 nn 个操作，操作涉及区间加法，询问区间内小于某个值 xx 的前驱（比其小的最大元素）。

输入格式

第一行输入一个数字 nn。

第二行输入 nn 个数字，第 ii 个数字为 a_iai，以空格隔开。

接下来输入 nn 行询问，每行输入四个数字 \mathrm{opt}opt、ll、rr、cc，以空格隔开。

若 \mathrm{opt} = 0opt=0，表示将位于 [l, r][l,r] 的之间的数字都加 cc。

若 \mathrm{opt} = 1opt=1，表示询问 [l, r][l,r] 中 cc 的前驱的值（不存在则输出 -1−1）。

输出格式

对于每次询问，输出一行一个数字表示答案。

样例

样例输入

1
2
3
4
5
6
4
1 2 2 3
0 1 3 1
1 1 4 4
0 1 2 2
1 1 2 4

样例输出

1
2
3
-1

数据范围与提示

对于 $100\%$的数据，$1 \leq n \leq 100000, -2^{31} \leq \mathrm{others} \leq 2^{31}$

题解

这道题，大概算是我写的最失败的一道题了吧。。

虽然和上面那道题几乎一模一样，主要是用vector+根号平衡来维护值单调从而实现二分查找等操作。

但是。。。我写的时候出了无数的bug，我顺便一一截图展示下。。

img

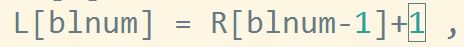
这里原来没有加1.。。

img

要想清楚变量的含义，别打的太快不过脑子。。

img

无话可说.jpg

img

最后一个错误，在最终的对拍后好不容易锁定了错误的位置。显然预处理的时候就得保证其块内有序。】

时间复杂度懒得写了，其实和上面一样，又其实所有这类平衡思想的题都可以类似的分析。

慢慢提高自己一边写对复杂代码的能力和调试的能力，确保自己在有思路的情况下不丢分，这非常重要。

上一下因调试代码导致无限长的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <vector>
#include <cmath>
#define _max 100005
#define _maxsqrt 320
int n , m , L[_maxsqrt] , R[_maxsqrt] , pos[_max] , blsize , blnum , a[_max] , tag[_max];

struct Node{
	int v , id;
	bool operator < (const Node& x)const{
		return v < x.v;
	}
};
std::vector<Node> bl[_maxsqrt];

inline void print(int l , int r)
{
	puts("ARRAY");
	static int tmp[_max];
	for(int i = 1 ; i <= blnum ; ++i)
	{
		for(int j = 0 ; j < (int)bl[i].size() ; ++j)
			tmp[bl[i][j].id] = bl[i][j].v;
	}
	for(int i = l ; i <= r ; ++i)
		printf("%d ",tmp[i] + tag[pos[i]]);
	puts("");
}


inline void pre()
{
	blsize = (int)std::pow(n,0.5);
	blnum = n / blsize;
	for(int i = 1 ; i <= blnum ; ++i)
		L[i] = (i-1)*blsize+1 , R[i] = i*blsize;
	if(R[blnum] < n) ++blnum , L[blnum] = R[blnum-1]+1 , R[blnum] = n;
	for(int i = 1 ; i <= blnum ; ++i)
		for(int j = L[i] ; j <= R[i] ; ++j)
			pos[j] = i , bl[i].push_back((Node){a[j],j});
	for(int i = 1 ; i <= blnum ; ++i)
		std::sort(bl[i].begin() , bl[i].end());
//	puts("PRE THE BLOCK INFO");
//	for(int i = 1 ; i <= blnum ; ++i)
//		printf("%d %d\n",L[i],R[i]);
}

inline void update(int l , int r , int v)
{
	if(pos[l] == pos[r])
	{
		for(int i = 0 ; i < (int)bl[pos[l]].size() ; ++i)
		{
			int id = bl[pos[l]][i].id;
			if(id >= l && id <= r)
				bl[pos[l]][i].v += v;
		}
		std::sort(bl[pos[l]].begin() , bl[pos[l]].end());
		return ;
	}

	int nl , nr;
	if(L[pos[l]] == l) nl = l;
	else nl = L[pos[l]+1];
	if(R[pos[r]] == r) nr = r;
	else nr = R[pos[r]-1];

	for(int i = 0 ; i < (int)bl[pos[l]].size() ; ++i)
	{
		int id = bl[pos[l]][i].id;
		if(id < nl && id >= l)
			bl[pos[l]][i].v += v;
	}
	std::sort(bl[pos[l]].begin() , bl[pos[l]].end());
	for(int i = 0 ; i < (int)bl[pos[r]].size() ; ++i)
	{
		int id = bl[pos[r]][i].id;
		if(id > nr && id <= r)
			bl[pos[r]][i].v += v;
	}
	std::sort(bl[pos[r]].begin() , bl[pos[r]].end());

	if(nl > nr) return;

	for(int i = pos[nl] ; i <= pos[nr] ; ++i)
		tag[i] += v;
	return ;
}


inline int find(std::vector<Node>& vec , int key)
{
	int l = 0 , r = (int)vec.size() - 1 , ans = -0x7fffffff;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(vec[mid].v < key) ans = vec[mid].v , l = mid + 1;
		else r = mid - 1;
	}
	return ans;
}



inline int query(int l , int r , int val)
{
//	printf("QUERY %d %d %d\n",l,r,val);
//	print(l,r);
	int ans = -0x7fffffff;
	if(pos[l] == pos[r])
	{
//		puts("THE QUERY SAME BLOCK!");
		for(int i = 0 ; i < (int)bl[pos[l]].size() ; ++i)
		{
			int id = bl[pos[l]][i].id , v = bl[pos[l]][i].v;
			if(id >= l && id <= r && v < val - tag[pos[l]]) ans = std::max(ans , v + tag[pos[l]]);
		}
		return ans;
	}

	int nl , nr;
	if(L[pos[l]] == l) nl = l;
	else nl = L[pos[l]+1];
	if(R[pos[r]] == r) nr = r;
	else nr = R[pos[r]-1];

//	if(l == 1 && r == 5 && val == 9){
//		printf("\n\nSPECIAL : %d %d\n\n",nl,nr);
//	}

	for(int i = 0 ; i < (int)bl[pos[l]].size() ; ++i)
	{
		int id = bl[pos[l]][i].id , v = bl[pos[l]][i].v;
		if(id < nl && id >= l && v < val - tag[pos[l]])
			ans = std::max(ans , v + tag[pos[l]]);
	}
//	if(l == 1 && r == 5 && val == 9){
//		printf("\n\nSPECIAL : %d\n\n",ans);
//	}
	for(int i = 0 ; i < (int)bl[pos[r]].size() ; ++i)
	{
		int id = bl[pos[r]][i].id , v = bl[pos[r]][i].v;
		if(id > nr && id <= r && v < val - tag[pos[r]])
			ans = std::max(ans , v + tag[pos[r]]);
	}
//	if(l == 1 && r == 5 && val == 9){
//		printf("\n\nSPECIAL : %d\n\n",ans);
//	}

	if(nl > nr) return ans;

	for(int i = pos[nl] ; i <= pos[nr] ; ++i)
	{
		int k = find(bl[i] , val-tag[i]);
//		if(l == 1 && r == 5 && val == 9){
//			puts("SPECIAL ARRAY");
//			for(int j = 0 ; j < (int)bl[i].size() ; ++j)
//				printf("%d ",bl[i][j].v);
//			puts("");
//			printf("SPECIAL THE BLOCK: %d ans: %d\n",i,k);
//		}
		if(k == -0x7fffffff) continue;
		ans = std::max(ans , k + tag[i]);
	}

	return ans;
}

int main()
{
//	freopen("data.in","r",stdin);
//	freopen("my.out","w",stdout);
	scanf("%d",&n);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&a[i]);
	pre();
	for(int i = 1 ; i <= n ; ++i)
	{
		int op , l , r , v;
		scanf("%d%d%d%d",&op,&l,&r,&v);
		if(op & 1){
			int now = query(l,r,v);
			printf("%d\n",now <=-0x6fffffff?-1:now);
		}
		else update(l,r,v);
	}
}

P3939 数颜色

题目背景

大样例下发链接：http://pan.baidu.com/s/1c0LbQ2 密码：jigg

题目描述

小 C 的兔子不是雪白的，而是五彩缤纷的。每只兔子都有一种颜色，不同的兔子可能有 相同的颜色。小 C 把她标号从 1 到 nn 的 nn 只兔子排成长长的一排，来给他们喂胡萝卜吃。 排列完成后，第 ii 只兔子的颜色是 a_iai。

俗话说得好，“萝卜青菜，各有所爱”。小 C 发现，不同颜色的兔子可能有对胡萝卜的 不同偏好。比如，银色的兔子最喜欢吃金色的胡萝卜，金色的兔子更喜欢吃胡萝卜叶子，而 绿色的兔子却喜欢吃酸一点的胡萝卜……为了满足兔子们的要求，小 C 十分苦恼。所以，为 了使得胡萝卜喂得更加准确，小 C 想知道在区间 [l_j,r_j][lj,rj] 里有多少只颜色为 c_jcj 的兔子。

不过，因为小 C 的兔子们都十分地活跃，它们不是很愿意待在一个固定的位置；与此同 时，小 C 也在根据她知道的信息来给兔子们调整位置。所以，有时编号为 x_jxj 和 x_j+1xj+1 的两 只兔子会交换位置。 小 C 被这一系列麻烦事给难住了。你能帮帮她吗？

输入输出格式

输入格式：

从标准输入中读入数据。 输入第 1 行两个正整数 nn,mm。

输入第 2 行 nn 个正整数，第 ii 个数表示第 ii 只兔子的颜色 a_iai。

输入接下来 mm 行，每行为以下两种中的一种：

  • “1\ l_j\ r_j\ c_j1 lj rj cj” ：询问在区间 [l_j,r_j][lj,rj] 里有多少只颜色为 c_jcj 的兔子；
  • “2\ x_j2 xj”： x_jxj 和 x_j+1xj+1 两只兔子交换了位置。

输出格式：

输出到标准输出中。

对于每个 1 操作，输出一行一个正整数，表示你对于这个询问的答案。

输入输出样例

输入样例#1：

复制

1
2
3
4
5
6
7
6 5 
1 2 3 2 3 3  
1 1 3 2 
1 4 6 3  
2 3 
1 1 3 2  
1 4 6 3

输出样例#1：

复制

1
2
3
4
1 
2 
2 
3

说明

【样例 1 说明】

前两个 1 操作和后两个 1 操作对应相同；在第三次的 2 操作后，3 号兔子和 4 号兔子

交换了位置，序列变为 1 2 2 3 3 3。

【数据范围与约定】

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。 对于所有测试点，有 1 \le l_j < r_j \le n,1 \le x_j < n1≤lj<rj≤n,1≤xj<n。 每个测试点的数据规模及特点如下表：

img

特殊性质 1：保证对于所有操作 1，有 |r_j - l_j| \le 20∣rj−lj∣≤20 或 |r_j - l_j| \le n - 20∣rj−lj∣≤n−20。

特殊性质 2：保证不会有两只相同颜色的兔子。

题解

这题似乎很容易就想到套路，搞不懂为啥有人非说这是思维题。

其实这道题让我练会了vector。。也不算练会，主要是知道vector引用怎么在函数里用和不能重赋值

还有vector指针调用各种东西得(*v)这样。。

说说这道题思路，把每种颜色的兔子开vector存位置（以前我第一次接触到这种思路也感觉：妙，,妙啊！，现在就觉得其实也不是很难想，主要是利用它只查询一个颜色的兔子这一点，总之就是抓住题目特点进行分析啦），然后位置单调不减。

所以我们每次查询二分小于，更新也二分就没了

然后vector的指针需要加括号！！

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <vector>
#define maxn 300005
std::vector<int> c[maxn];
int n , m , p[maxn];

inline void print(const std::vector<int>& v){
	puts("THE ARRAY");
	printf("size: %d\n",v.size());
	for(int i = 0 ; i < (int)v.size(); ++i)
		printf("%d ",v[i]);
	puts("");
}

inline int calc(const std::vector<int>& v , int ql , int qr)
{
	int l = 0 , r = (int)v.size() - 1 , ans1 = 0 , ans2 = 0;
	if(!v.size()) return 0;
	if(v[r] < ql || v[l] > qr) return 0;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(v[mid] <= qr) ans1 = mid , l = mid + 1;
		else r = mid - 1;
	}
	
	l = 0 , r = (int)v.size() - 1;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(v[mid] >= ql) ans2 = mid , r = mid - 1;
		else l = mid + 1;
	}
	return ans1 - ans2 + 1;
}


inline void update(int pos)
{
	if(p[pos] == p[pos+1]) return ;
	int c1 = p[pos] , c2 = p[pos+1];
	std::swap(p[pos],p[pos+1]);

	std::vector<int>& v = c[c1];
	int l = 0 , r = (int)v.size() - 1 , ans = 0;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(v[mid] <= pos) ans = mid , l = mid + 1;
		else r = mid - 1;
	}
	v[ans] = pos + 1;

	std::vector<int>& vec = c[c2];
	l = 0 , r = (int)vec.size() - 1 , ans = 0 ;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(vec[mid] <= pos + 1) ans = mid , l = mid + 1;
		else r = mid - 1;
	}
	vec[ans] = pos;
}



int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1 ; i <= n ; ++i)
	{
		int x; 
		scanf("%d",&x);
		p[i] = x;
		c[x].push_back(i);
	}
	for(int i = 1 ; i<= m ; ++i)
	{
		int op , l , r , k;
		scanf("%d",&op);
		if(op == 1)
		{
			scanf("%d%d%d",&l,&r,&k);
			printf("%d\n",calc(c[k],l,r));
		}
		else {
			scanf("%d",&k);
			update(k);
		}

	}
}

这种难度的还是随便切的。

关于vector

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <vector>
#define maxn 100004
std::vector<int> g[maxn];
int main()
{
	g[2].push_back(2),g[2].push_back(3);
	std::vector<int>* v = &g[2];
	v -> operator[](2);
	(*v).push_back(23);
	std::cout<<g[2][0];
}

不过还是不要用->了，也不浪费时间去研究那个东西了

今天就到此为止，听会歌再说