Post 31

Veröffentlicht am

人们说当你遇上你的挚爱时，时间会暂停。真的是这样。但人们没有告诉你，当时针再度恢复转动，它会无比飞快，让人无法赶上。

[2009国家集训队]小Z的袜子(hose)

Description

作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命……
具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择。

Input

输入文件第一行包含两个正整数N和M。N为袜子的数量，M为小Z所提的询问的数量。接下来一行包含N个正整数Ci，其中Ci表示第i只袜子的颜色，相同的颜色用相同的数字表示。再接下来M行，每行两个正整数L，R表示一个询问。

Output

包含M行，对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/1，否则输出的A/B必须为最简分数。（详见样例）

Sample Input

6 4
1 2 3 3 3 2
2 6
1 3
3 5
1 6

Sample Output

2/5
0/1
1/1
4/15

【数据规模和约定】
$100\%$的数据中 $N,M ≤ 50000，1 ≤ L < R ≤ N，Ci ≤ N$。

题解

又是一个很裸的莫队，做完这道就开始练习带修莫队啦（HH的项链，[C. color][http://noi.ac/contest/15/problem/44]等等）

这道题只需要说下$O(1)$修改（其他好像很模板，怪不得很多人都背板子），对于每个加入的颜色。

对$curans$的贡献：$2c(v(x))$

但是减少一个的贡献可不是把它反过来，一定要自己推一下是：
$-2c(v(x))+2$

然后就没有然后了，以后莫队都写左闭右开了。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cmath>
#define maxn 50005
int n , m , c[maxn] , bl , v[maxn];
long long ans[maxn] , tot[maxn] , curans;
struct node
{
	int l , r , id;
	bool operator<(const node& x)const{
		if(l/bl == x.l/bl) return r < x.r;
		return l/bl < x.l/bl;
	}
}q[maxn];

inline void update(int col , int ty)
{
	if(ty == 1)
		curans += 2*c[v[col]];
	else curans += 2 - 2 * c[v[col]];
	c[v[col]] += ty;
}

inline void solve()
{
	bl = (int)std::pow(n,0.67);
	std::sort(q+1,q+m+1);
	for(int i = 1 ; i <= m ; ++i) q[i].r ++;
	int l = 1 , r = 1;
	for(int i = 1 ; i <= m ; ++i)
	{
		while(l > q[i].l) update(--l, 1);
		while(r < q[i].r) update(r++ , 1);
		while(l < q[i].l) update(l++ , -1);
		while(r > q[i].r) update(--r , -1);
		ans[q[i].id] = curans , tot[q[i].id] = 1ll * (q[i].r - q[i].l) * (q[i].r-q[i].l-1);
	}
}

int gcd(long long x , long long y){
	if(!y)	return x;
	return gcd(y , x % y);
}

int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&v[i]);
	for(int i = 1 ; i <= m ; ++i)
		scanf("%d%d",&q[i].l,&q[i].r) , q[i].id = i;
	solve();
	for(int i = 1 ; i <= m ; ++i)
	{
		if(ans[i] == 0) puts("0/1");
		else printf("%lld/%lld\n",ans[i]/gcd(ans[i],tot[i]) , tot[i]/gcd(ans[i],tot[i]));
	}
}

[国家集训队]数颜色 / 维护队列

题目描述

墨墨购买了一套N支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：

1、 Q L R代表询问你从第L支画笔到第R支画笔中共有几种不同颜色的画笔。

2、 R P Col 把第P支画笔替换为颜色Col。

为了满足墨墨的要求，你知道你需要干什么了吗？

输入输出格式

输入格式：

第1行两个整数N，M，分别代表初始画笔的数量以及墨墨会做的事情的个数。

第2行N个整数，分别代表初始画笔排中第i支画笔的颜色。

第3行到第2+M行，每行分别代表墨墨会做的一件事情，格式见题干部分。

输出格式：

对于每一个Query的询问，你需要在对应的行中给出一个数字，代表第L支画笔到第R支画笔中共有几种不同颜色的画笔。

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
6 5
1 2 3 4 5 5
Q 1 4
Q 2 6
R 1 2
Q 1 4
Q 2 6

输出样例#1：

1
2
3
4
4
4
3
4

说明

对于$100\%$的数据，$N≤50000，M≤50000$，所有的输入数据中出现的所有整数均大于等于1且不超过$10^6$。

题解

调出第一道带修莫队。

话说有个滑稽的错误让我正好一眼看出来了，然后就过了，如下：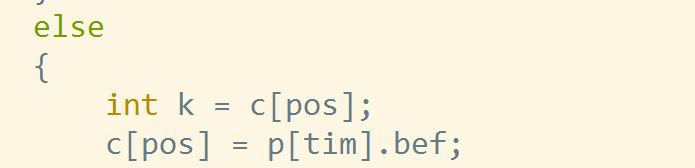
img

原来的时候我把这两个写反了可还行。。。

然后就很简单了，显然理解这个算法后基本上都是一样的东西了。

虽然号称解决一切序列问题，但是带修莫队真！的！很！慢！

我们在之前已经推导过带修莫队的各种理论了，最优块大小是$n^{\frac{2}{3}}$

但是据说小一点会更快。。

我们按照三元组排序然后暴力就行了。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cmath>
#define maxn 50005
#define maxv 1000005
int n, m , c[maxn] , tot1 , tot2 , ans[maxn] , b[maxv] , bl , curans , tmp[maxv];
struct Query
{
	int l , r , t, id;
	bool operator < (const Query& x)const{
		if(l/bl == x.l/bl && r/bl == x.r/bl) return t < x.t;
		if(l/bl == x.l/bl) return r/bl < x.r/bl;
		return l/bl < x.l/bl;
	}
}q[maxn];

struct Modify{
	int p , v , bef;
}p[maxn];

inline void update(int p , int ty)
{
	if(ty == 1)
	{
		b[c[p]] ++ ;
		if(b[c[p]] == 1)	++curans;
	}
	if(ty == -1)
	{
		b[c[p]] -- ;
		if(!b[c[p]]) --curans;
	}
}

inline void updTime(int tim , int ty , int l , int r)
{
	int pos = p[tim].p;
	if(ty == 1)
	{
		int k = c[pos];
		c[pos] = p[tim].v;
		if(pos >= l && pos < r)
		{
			b[c[pos]] ++ ;
			if(b[c[pos]] == 1) ++curans;
			b[k] --;
			if(!b[k]) --curans;
		}
	}
	else
	{
		int k = c[pos];
		c[pos] = p[tim].bef;
		if(pos >= l && pos < r)
		{
			b[c[pos]] ++;
			if(b[c[pos]] == 1) ++curans;
			b[k] --;
			if(!b[k]) --curans;
		}
	}
			
}

inline void print(int l , int r , int op)
{
	if(op == 1)
	{
		puts("ARRAY:");
		for(int i = l ; i <= r ; ++i)
			printf("(%d,%d) ",c[i],b[c[i]]);
		puts("");
	}
	printf("l:%d r:%d CURANS : %d\n",l,r,curans);
}


inline void solve()
{
	bl = (int)std::pow(n , 0.67);
	std::sort(q+1,q+tot1+1);
	int l = 1 , r = 1 , t = 0;	
	for(int i = 1 ; i <= tot1 ; ++i)
		++ q[i].r;

	for(int i = 1 ; i <= tot1 ; ++i)
	{
//		printf("THE %d query started : %d %d %d\n",q[i].id ,q[i].l,q[i].r,q[i].t);
		while(t < q[i].t) updTime(++t,1,l,r) ;//, print(q[i].l,q[i].r,1);
		while(t > q[i].t) updTime(t--,-1,l,r) ;//, print(q[i].l,q[i].r,1);
		while(l < q[i].l) update(l++ , -1); //, print(l,r,0);
		while(l > q[i].l) update(--l , 1); //,  print(l,r,0);
		while(r < q[i].r) update(r++ , 1) ;//, print(l,r,0);
		while(r > q[i].r) update(--r , -1); //, print(l,r,0);
//		printf("THE %d query %d %d finished\n",q[i].id,l,r);
		ans[q[i].id] = curans;
	}
}



inline void pre()
{
	for(int i = 1 ; i <= n ; ++i)
		tmp[i] = c[i];
	for(int i = 1 ; i <= tot2 ; ++i)
	{
		int pos = p[i].p;
		p[i].bef = tmp[pos];
		tmp[pos] = p[i].v;
	}
}


int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&c[i]);
	for(int i = 1 ; i <= m ; ++i)
	{
		char op;
		scanf("\n%c",&op);
		if(op == 'Q')
			++tot1 , scanf("%d%d",&q[tot1].l,&q[tot1].r) , q[tot1].id = tot1 , q[tot1].t = tot2;
		else if(op == 'R') ++tot2 , scanf("%d%d",&p[tot2].p,&p[tot2].v);
	}
	pre();
	solve();
	for(int i = 1 ; i <= tot1 ; ++i)
		printf("%d\n",ans[i]);
}

今天莫队就做到这里吧，看道POI思维题。

[POI2005]DWU-Double-row

Description

2n 个士兵站成两排. 他们必须重新排列使得任意一排都没有两个相同高度的士兵. 只可以进行一种操作即交换一列中的两个士兵. 你的任务是确定最少要进行多少次操作才能达到要求. Example: 图中所示的是18 个士兵站成了2排. 按图中的方式进行操作.

Input

第一行一个数n, 1 <= n <= 50 000. 接下来两行每行n个数表示对应列的士兵的高度x1, x2,…, xn, 1 <= xi <= 100 000; y1, y2,…, yn, 1 <= y <= i100 000. 数据保证一定存在一组方案使得可以达到目标.

Output

一行输出一个数字表示最少操作数.

题解

太失败了，最后也只得到了40分。。

确实联想到了二分图，但是考虑的情况不够全面。

我是这么想的，假如我们把上下都是有同行重复的元素连边，然后求每个联通块size，然后统计答案。

这样显然是错误的，因为有可能把本来相同的不在同一行的给交换过来然后就错了，所以答案会比实际答案更优。

所以我们应该这么建二分图：还是只考虑相同元素，不过相同元素在同一行的话向另一行对应下标的元素连边权为1的边，在不同的行连边权为0的边，对每个联通块（必定二分图）BFS，每次过边权为1的边需要换颜色，边权为0的不换颜色，这样就让不同行的要么同时换要么同时不换，就正确了。

恩就这样，不想Code.

#1468. Tree

Description

给你一棵TREE,以及这棵树上边的距离.问有多少对点它们两者间的距离小于等于K

Input

N（n<=40000） 接下来n-1行边描述管道，按照题目中写的输入 接下来是k

Output

一行，有多少对点之间的距离小于等于k

Sample Input

7

1 6 13

6 3 9

3 5 7

4 1 3

2 4 20

4 7 2

10

Sample Output

5

题解

这题挺好写啊。。。简单容斥原理就行了，不知道进阶指南上的扫描数组是个什么鬼。。。

还是自己想的写的好。

思路的话在我的Post 26中写了，所以我还是要复制一遍233

假如了解过点分治不难想到做法。

对于这种统计路径并且对于一个点p能分治成过p和不过p的，可以很容易联想到点分治做法。

  • 求出当前树的重心
  • dfs求出每个点到当前重心的距离，排序后用双指针扫描统计，注意容斥，把重心每个子树在这样做一遍即可
  • 递归每个子树重心（注意，如果递归的点已经被访问，代表已经被处理，返回即可。）

整个做法的时间复杂度是$O(nlog^2n)$

第二步的容斥网上都讲的繁琐玄学。。。然后我就想到这个方法，可能慢一点但很好理解，就代表去掉相同子树里的点对（不属于简单路径）。

还有就是为什么递归重心最多只需要$logn$次，给出证明：

这个命题等价于将重心删除后，最大联通块小于等于树大小的一半，这里我们可以反证。

如果最大联通块的大小超过一半，那么其它的加起来小于一半，此时重心取那个最大联通块与当前重心相连的点时比当前重心优，即当前重心不满足重心定义，与初始条件矛盾。所以

最大联通块小于等于树大小的一半。

然后就没什么了。

考虑点分治奇多无比的细节与今天阴暗的内心世界，我决定咕掉代码。

然后现在补上了代码，调试代码见证我的努力

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <vector>
#define maxn 100005
#define LL long long
int n , k , root , now , ct , sz[maxn] , d[maxn] , ans;

struct Node{
	int x , v;
};
std::vector<Node> g[maxn];

void getroot(int x , int fx)
{
	int maxx = 0x7fffffff;
	sz[x] = 1;
	for(int i = 0 ; i < (int)g[x].size() ; ++i)
	{
		int v = g[x][i].x;
		if(v == fx) continue;
		getroot(v , x);
		sz[x] += sz[v];
		maxx = std::max(maxx , sz[v]);
	}
	maxx = std::max(maxx , n - sz[x]);
	if(maxx < now)
	{
		now = maxx;
		root = x;
	}
}


void getDis(int x , int fx , int dis)
{
	d[++ct] = dis;
	for(int i = 0 ; i < (int)g[x].size() ; ++i)
	{
		int v = g[x][i].x;
		if(v == fx) continue;
		getDis(v , x , dis + g[x][i].v);
	}
}

inline void calc(int rt , int fx)
{
//	printf("NOW THE ROOT:%d Father:%d\n",rt,fx);
	ct = 0;
	getDis(rt , fx , 0);
	std::sort(d+1,d+ct+1);
//	puts("THE TREE PRESUM");
//	for(int i = 1 ; i <= ct ; ++i)
//		printf("%d ",d[i]);
//	puts("");
	
//	int t = ans;
	int l = 1 , r = ct;
	while(l < r)
	{
		while(d[l] + d[r] > k) --r;
		if(l >= r) break;
		ans += r - l ;
		++l;
	}

//	printf("THE CONBINATE WHICH NOT UNIQUE : %d\n", ans-t);

	for(int i = 0 ; i < (int)g[rt].size() ; ++i)
	{
//		int t = ans;
		int v = g[rt][i].x;
		if(v == fx) continue;
		ct = 0;
		getDis(v , rt , g[rt][i].v);
		std::sort(d+1,d+ct+1);
//		puts("UNIQUE FROM SUBTREE");
//		for(int j = 1 ; j <= ct ; ++j)
//			printf("%d ",d[j]);
//		puts("");
		int l = 1, r = ct;
		while(l < r)
		{
			while(d[l] + d[r] > k) --r;
			if(l >= r) break;
			ans -= r - l ;
			++l;
		}
//		printf("THE ILLEGAL FROM SON:%d is:%d\n",v,t-ans);
	}

}
	



void TreeDC(int rt , int fx)
{
	calc(rt , fx);

	for(int i = 0 ; i < (int)g[rt].size() ; ++i)
	{
		int v = g[rt][i].x;
		if(v == fx) continue;
		getroot(v , rt);
		TreeDC(v , rt);
	}

}

int main()
{
	scanf("%d",&n);
	for(int i = 1 ; i < n ; ++i)
	{
		int x , y , d;
		scanf("%d%d%d",&x,&y,&d);
		g[x].push_back((Node){y,d});
		g[y].push_back((Node){x,d});
	}
	
	scanf("%d",&k);
	TreeDC(1,1);

	printf("%d\n",ans);
}