Post 27

Veröffentlicht am

我爱过你，利落干脆

复习一下EXCRT吧！

img

顺便贴下我以前的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// luogu-judger-enable-o2
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 100005
#define ll long long
ll A[maxn] , B[maxn] , n;
ll exgcd(ll a , ll b , ll& x, ll& y)
{
    if(!b)
    {
        x = 1 , y = 0;
        return a;
    }
    ll g = exgcd(b , a % b , y, x);
    y -= a/b * x;
    return g;
}
inline ll mul(ll x , ll y , ll mod)
{
    ll ans = 0 , base = x;
    while(y)
    {
        if(y & 1)   ans = (ans + base) % mod;
        (base <<= 1 ) %= mod;
        y >>= 1;
    }
    return ans;
}
ll EXCRT()
{
    ll ans = A[1] , P1 = B[1] , x , y;//init first equation
    for(int i = 2 ; i <= n ; ++i)
    {
        ll a = P1 , b = B[i] , c = (A[i] - ans % b + b) % b  , gcd = exgcd(a,b,x,y) , poc = b / gcd;
        x = mul(x , c / gcd , poc);
        x = (x + poc) % poc; // make sure x is a positive integer
        if(c % gcd) return -1;

        ans += x * P1;
        P1 *= poc;
        ans = (ans % P1 + P1) % P1;
    }
    return ans;
}
int main()
{
    scanf("%lld",&n);
    for(int i = 1 ; i <= n ; ++i)
        scanf("%lld%lld",&B[i],&A[i]);
    printf("%lld",EXCRT());
}

模数LCM需要小于long long范围（实在不行只能写高精度这种恶心的东西了）

顺便看下Lucas定理（又是抄袭）：

卢卡斯定理

我的大部分式子都是展开形式就是一堆没有的展开

首先我们需要证明$C_p^i\equiv\frac{p}{i}C_{p-1}^{i-1}\equiv 0~~~(mod~p),(1<=i<=p-1)$

$C_p^i=\frac{p!}{i!(p-i)!}=\frac{p}{i} \frac{(p-1)!}{(i-1)!(p-1-i+1)!} \frac{p}{i} \frac{(p-1)!}{(i-1)!(p-i)!}=\frac{p}{i}C_{p-1}^{i-1}$

得证。

然后根据这种性质和二项式定理。，我们马上得出

$(1+x)^p\equiv C_p^01^p+C_p^1x^{2}+….+C_p^px^p\equiv C_p^01^px^0+C_p^p1^0x^p\equiv 1+x^p(mod ~p)$

然后我们接下来要求证

$C_a^b\equiv C_{a_0}^{b_0}\cdot C_{a_1p}^{b_1p} \cdot C_{a_2p^2}^{b_2p^2}…..(mod~p)$

其实我们令$a=lp+r,b=sp+j$好奇怪的变量名呀,随便起的~~

求证$C_a^b\equiv C_{lp}^{sp}\cdot C_{r}^{j}(mod~p)$然后利用性质递归求解就可以了。

继续从二次项定理出发

$(1+x)^a=(1+x)^{lp} \cdot (1+x)^r$

然后展开$(1+x)^{lp}$

$(1+x)^{lp} \equiv ((1+x)^p)^l \equiv (1+x^p)^l(mod~p)$

$\therefore (1+x)^a \equiv (1+x^p)^l \cdot (1+x)^r(mod~p)$

观察项$x^b$的系数

$\because C_a^bx^b \equiv C_l^sx^{sp} \cdot C_r^jx^j(mod~p)$

$\therefore C_a^bx^b \equiv C_l^s \cdot C_r^jx^b(mod~p)$

$\therefore C_a^b\equiv C_l^s\cdot C_r^j \equiv C_{\lfloor \frac{a}{p} \rfloor}^{\lfloor \frac{b}{p} \rfloor}\cdot C_{a~mod~p}^{b~mod~p}(mod~p)$

//上面的取模写法好像不大严谨，还请见谅（并没有系统的学过同余）

得证

实现的时候注意可能出现计算组合数m比n大的情况，这个时候需要返回0不然会算错

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 100005
#define ll long long
ll n , m , k;
int t;

int exgcd(int a, int b , int& x , int& y)
{
	if(!b){
		x = 1 , y = 0;
		return a;
	}
	int g = exgcd(b , a % b , y, x);
	y -= a/b * x;
	return g;
}

inline int inv(int num)
{
	int x , y , gcd = exgcd(num , k , x , y);
	x = (x % k + k) % k;
	return x;
}

inline ll C(int x , int y)
{
	ll ans = 1;
	if(y > x) return 0;
	for(int i = y + 1 ; i <= x ; ++i)
		(ans *= i) %= k;
	for(int i = 1 ; i <= x - y ; ++i)
		(ans *= inv(i)) %= k;
	return ans;
}

inline ll lucas(int x , int y)
{
	if(!y) return 1;
	ll ans = 1;
	return C(x % k , y % k) * lucas(x / k , y / k) % k;
}
int main()
{
	scanf("%d",&t);
	while(~--t)
	{
		scanf("%lld%lld%lld",&n,&m,&k);
		printf("%lld\n",lucas(n+m,m));
	}
}

然后愉快的看ExLucas原理

扩展卢卡斯定理。

首先，得确定先会扩展欧几里得算法和扩展中国剩余定理。至于卢卡斯定理，那并不重要。

设$p=\prod p_i^{k_i}$，则:

假如你已经求出了$\binom{n}{m}\bmod{p_i^{k_i}}$，那么明显是可以利用exCRT来合并答案的。

那么问题转换为如何求出$\binom{n}{m}\bmod{p^k}$(p是质数)。

可以知道:$\binom{n}{m}=\frac{n!}{m!(n-m)!}$那么问题即转化为求出几个阶乘和阶乘的逆元。

现在，问题归为如何快速求出阶乘。

为了便于统计出现了多少个$p$的次幂，先将阶乘中所有p的倍数提出来。可以简单算出，一共有$\displaystyle\lfloor\frac{n}{p}\rfloor$个。这中间每一项都除去p，可以得到$\displaystyle\lfloor\frac{n}{p}\rfloor!$。该部分可以选择递归求解。

那么接下来只剩下非$p$的倍数的几项了。通过简单观察可以知道（这里很玄学），剩余几项具有循环节，循环节长度小于$p^k$。原因是剩余项关于$p$具有循环节，而$a+p^k\equiv a\pmod{p^k}$，所以可以一起计算。结果会剩下几项凑不齐一个循环节，但是这几项长度已经小于一个循环节了，可以选择暴力求解。

为了更好地理解上方几条，可以举个栗子:

img

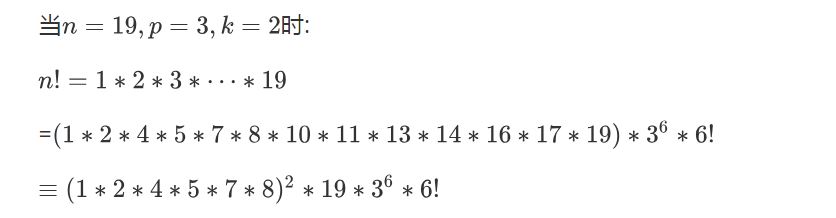
这样就可以在可承受的时间复杂度内求出阶乘。但是，为了达到除法的效果，我们需要考虑$p$的次幂一共出现了多少次。根据前面的计算，可以知道只除去一个$p$时，$n!$内包括了$\displaystyle\lfloor\frac{n}{p}\rfloor$个$p!$。剩下的数字如果要可能存在$p$的次幂也可以归为一个阶乘，即$\displaystyle\lfloor\frac{n}{p}\rfloor$!。设$f(n)$表示$n!$中有多少个$p$的因数，那么，我们就可以得到一个递推式$f(n)=f(\displaystyle\lfloor\frac{n}{p}\rfloor)+\displaystyle\lfloor\frac{n}{p}\rfloor$边界为:$f(x)=0(x<p)$

开始计算时间复杂度。

首先是中国剩余定理的复杂度，是$O(plogP)$的。(其中P是模数，p是最大质因子)。

然后是求阶乘复杂度。当求$n!\bmod p^k$时，时间复杂度为$O(p^klogn(log_pn-k))$

最后是求逆元的复杂度。利用扩展欧几里得可以做到$O(logp)$

因此，总复杂度为$O(\sum p^klogn(log_pn-k)+plogP)$

这个复杂度和$O(PlogP)$同级。

献上因为写完10分钟，有个函数没开$ll$调了两小时的玄学EXLUCAS模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
// luogu-judger-enable-o2
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 1000005
#define ll long long

ll n , m , mod;
ll exgcd(ll a , ll b , ll& x , ll& y)
{
    if(!b){
        x = 1 , y = 0 ; return a;
    }
    ll g = exgcd(b , a % b , y , x);
    y -= a/b * x;
    return g;
}

inline ll inv(ll a , ll mod)
{
    ll x , y , gcd = exgcd(a , mod , x , y);
    x = (x % mod + mod) % mod;
    if(!x) x += mod;
    return x;
}

inline ll pow(ll x, ll y , ll mod)
{
    ll ans = 1 , base = x;
    while(y)
    {
        if(y & 1) ans = (ans * base) % mod;
        base = (base * base) % mod;
        y >>= 1;
    }
    return ans;
}

ll f(ll x , ll p)
{
    if(x < p) return 0;
	ll ans = f(x/p , p);
	return ans + x / p;
}

inline ll fac(ll n , ll pi , ll pk)
{
    if(!n) return 1;
    ll ans = 1;
    if(n / pk){
        for(int i = 2 ; i <= pk ; ++i)
            if(i % pi) (ans *= i) %= pk;
        ans = pow(ans , n / pk , pk);
    }
    for(int i = 2 ; i <= n % pk ; ++i)
        if(i % pi) (ans *= i) %= pk;
    return ans * fac(n / pi , pi , pk) % pk;
}

inline ll C(ll n , ll m , ll pi , ll pk)
{
    if(m > n) return 0;
    ll k = f(n , pi) - f(m , pi) - f(n-m , pi);
    ll a = fac(n , pi , pk) , b = fac(m , pi , pk) , c = fac(n - m , pi , pk);
   	return a * inv(b , pk) % pk * inv(c , pk) % pk * pow(pi , k , pk) % pk;
}

inline ll CRT(ll x , ll pk){
    return x * (mod / pk) % mod * inv(mod / pk , pk) % mod;
}

inline ll exlucas(ll n , ll m)
{
    ll ans = 0;
    for(ll tmp = mod , i = 2 ; i <= mod ; ++i)
    {
        if(tmp % i == 0)
        {
            int pk = 1;
            while(!(tmp % i)) pk *= i , tmp /= i;
            (ans += CRT(C(n , m , i , pk) , pk)) %= mod;
        }
    }
    return ans;
}

int main()
{
    scanf("%lld%lld%lld",&n,&m,&mod);
    printf("%lld\n",exlucas(n,m));
    return 0;
}

在写exlucas之前我们最好学习一下CRT(中国剩余定理)，这样exlucas的代码量就可以少一点。

中国剩余定理

img

我们如何证明它的正确性呢？
img

这样我们只需要看看如何通过上述定理合并两个同余方程。

1
inline ll CRT(ll b,ll mod){return b*inv(p/mod,mod)%p*(p/mod)%p;}

p是所有模数乘起来（就是所有mod乘起来），mod是当前模数，然后就是上面一模一样的定理。我们可以用这个在$O(logn)$的时间里合并同余方程（各模数互质）。

然后就可以补上最上面那个玄学定理（没有确定的时间复杂度和正确性保证。。）的题解代码。

简单的扩欧写法：

1
2
3
4
5
void exgcd(LL a,LL b,LL &x,LL &y)
{
    if (!b) x=1LL,y=0LL;
    else exgcd(b,a%b,y,x),y-=a/b*x;
}

数论题有的地方忘了开long long调试真是痛苦的事情。。。。

幸好debug能力变强了一点，不过还是看了2小时。。。。以后用long long就全用得了。。

总结：四个有趣的数论定理回顾了一下，EXLUCAS玄学算法无正确性证明，我还是那么菜。