Post 22

Veröffentlicht am | Edited on

我们总是东张西望，唯独漏了自己想要的，这就是我们至今难以如愿以偿的原因。

有时候我们需要单点修改区间查询的小常数线段树，这就是zkw线段树。

zkw整个学习时间不超过5分钟。

zkw线段树学习笔记

Note：注意使用位运算优化常数。

zkw线段树建树的方式就是首先输入叶子结点的信息然后再一路向上传递信息，直到根结点。这时问题又来了….Where is the first leaf？？？我怎么找到第一个叶子在哪？假设我们的单点数量（叶子数量）正好是 $2^k$ ，那么我们手里就握着一个满二叉树了，这样我们就能轻松地计算出来第一个结点的位置是： $2^{k}$ 。但是如果不是满二叉树怎么办呢？没有关系，现在的电脑内存不是问题！直接开成满二叉树就好啦~~。这样一来，第一个叶子结点的位置就是： $2^k+1(k=\lceil\log_2N\rceil)$

(见代码下的解释)，也就是比 N 大的最小的 $2^k$。找到叶子结点之后，直接输入叶子结点信息，然后一个一个结点上传信息到父亲结点。于是我们得到了这样的代码：

1
2
3
4
5
6
7
8
9
inline void Maintain(int x) {
    tree[x] = tree[x<<1] + tree[x<<1|1];
}

inline void Build() {
    for(M=1;M<N;M<<=1);
    for(int i=M+1;i<=M+N;++i) scanf("%d", &tree[i]);
    for(int i=M-1;i;--i) Maintain(i);
}

简洁明了，注意从M+1开始比较好

NOTICE：看到评论中很多朋友问为什么要在 $M+1$ 处开始输入。我这里统一解释一下，评论中我所说的也有问题(这里说声抱歉，昨天一天都在路上，没有时间思考….)，以文章此处为标准好啦。

建议先看完下一节（区间和计算）再来看此处有助于理解。从 $M+1$开始是为了进行区间查询。

假设我们查询的区间就是 [1,N] ，这时为了进行查询我们会将 [1,N] 转换为 (0,N-1) ，看上去没有区别，其实是有区别的。由于位于 0 上的数字是否能被统计上与左端点位置相关$L=M+1-1=M$，如果从 M 开始输入会导致查询时统计不到位于 0 上的信息，因为 L 初始位置就是第一个叶子的位置了$L=M$ .. 但是如果换成 M+1 开始，查询时 L 的位置依旧是 $L=M+1-1=M$ ，但是第一个叶子的位置在 $M+1 $上，这样就能够统计到那个叶子上的信息啦。因此要从 $M+1 $ 开始输入信息。

更新操作不难，就是直接找到叶子然后向上pushup即可

1
2
3
4
5
inline void Update(int pos,int v) {
    pos += M;
    tree[pos] = v;
    for(pos>>=1;pos;pos>>=1) Maintain(pos);
}

接下来是略有难度的区间查询

我们需要把L,R分别向左向右一个位置，然后查询。

Q：为什么？

Ans：就是得这样啊。。不然你端点开始就查错了。查询原理如下：

当遇到区间和查询时，问题双来了….传统线段树通过递归查询需要加和的区间最后统计所有的和，但是Zkw线段树….没法从顶上找到需要加和的区间啊QwQ….怎么办呢？但是换个方向思考…从底向上，查询区间为 $[L,R]$，我们只能知道当前区间是否在查询区间内，即：如果当前查询区间左端点 $L$向结点是线段树某个结点的左儿子且 $R-1 \ne L$(即右端点指向结点不是左端点指向结点的兄弟)，那么它的兄弟结点$ L+1$ 必然在查询区间内。同理，如果 $R$所指向结点的兄弟结点不是$L$，那么它的兄弟结点必然包含在查询区间内。如图：

zkw

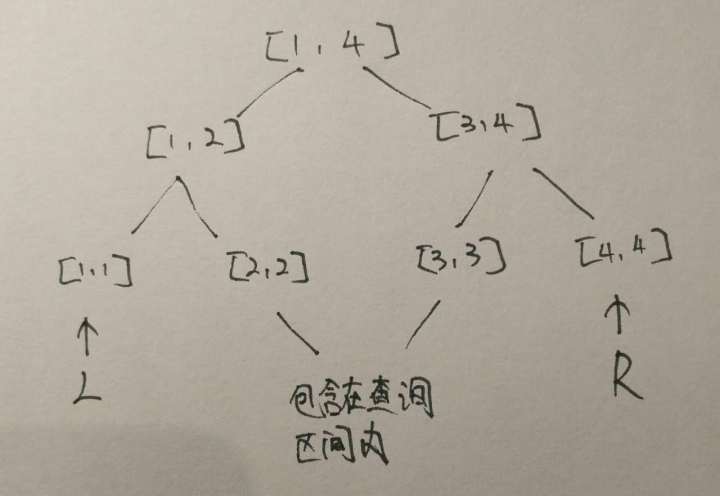
讲真这个东西确实不是很自然，主要是考虑$1$~$n$查询，其边界这样做依旧正确，就行了。

1
2
3
4
5
6
7
8
9
10
11
12
inline int Sum(int l,int r) {
    int ans = 0;
    // l=l+M-1->将查询区间改为L-1，r=r+M+1->将查询区间改为R+1
    // l^r^1 -> 相当于判断l与r是否是兄弟节点
    for(l=l+M-1,r=r+M+1;l^r^1;l>>=1,r>>=1) {
        if(~l&1) // l % 2 == 0 即l是l/2的左儿子
            ans += tree[l^1];
        if(r&1) // r % 2 == 1 即r是r/2的右儿子
            ans += tree[r^1];
    }
    return ans;
}

这样zkw线段树就基本上介绍完毕了，可以试试优化天使玩偶了！

果然依靠zkw线段树在72秒内跑过了

不过还要在想想zkw的各种边界。

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cstring>
#define maxn 500005
#define maxv 1000005
#define INF 0x7ffffff
int ans[maxn<<1] , n , m , seg[maxv<<2] , mx , base;
inline void pushup(int x){
	seg[x] = std::max(seg[x<<1] , seg[x<<1|1]);
}
inline void build(){
	for(base = 1 ; base < mx ; base <<= 1);
	for(int i = base ; i <= base + mx ; ++i) seg[i] = -INF;
	for(int i = base - 1; i ; --i) seg[i] = -INF;
}
inline void update(int pos , int v)
{
	pos += base;
	seg[pos] = v;
	for(pos >>= 1; pos ; pos >>= 1) pushup(pos);
}
inline int query(int L , int R)
{
	int ans = -INF;
	for(int l = L + base - 1 , r = R + base + 1 ; l ^ r ^ 1 ; l >>= 1 , r >>= 1)
	{
		if(~l&1) ans = std::max(ans , seg[l^1]);
		if(r&1) ans = std::max(ans , seg[r^1]);
	}
	return ans;
}
struct Node{
	int x , y , ty ,num;
	bool operator<(const Node& k)const{
		if(x == k.x) return ty < k.ty;
		return x < k.x;
	}
}q[maxn<<1] , tmp[maxn<<1];
bool cmp(const Node& a , const Node& b){
	if(a.x == b.x) return a.ty < b.ty;
	return a.x > b.x;
}
inline void solve(int l , int r)
{
	if(l == r) return;
	int mid = l + r >> 1;
	solve(l , mid);
	solve(mid + 1, r);
	for(int i = l ; i <= r ; ++i)
		tmp[i] = q[i];
		
	std::sort(tmp+l,tmp+r+1);
	for(int i = l ; i <= r ; ++i)
	{
		if(tmp[i].ty == 1 && tmp[i].num <= mid) update(tmp[i].y , tmp[i].x + tmp[i].y);
		else if(tmp[i].ty == 2 && tmp[i].num > mid)	
			ans[tmp[i].num] = std::min(ans[tmp[i].num] , tmp[i].x + tmp[i].y - query(0 , tmp[i].y));
	}
	for(int i = l ; i <= r ; ++i)
		if(tmp[i].ty == 1 && tmp[i].num <= mid) update(tmp[i].y , -INF);


	for(int i = l ; i <= r ; ++i)
	{
		if(tmp[i].ty == 1 && tmp[i].num <= mid) update(tmp[i].y , tmp[i].x - tmp[i].y);
		else if(tmp[i].ty == 2 && tmp[i].num > mid) ans[tmp[i].num] = std::min(ans[tmp[i].num] , tmp[i].x - tmp[i].y - query(tmp[i].y,mx));
	}
	for(int i = l ; i <= r ; ++i)
		if(tmp[i].ty == 1 && tmp[i].num <= mid) update(tmp[i].y , -INF);
		

	std::sort(tmp+l,tmp+r+1,cmp);
	for(int i = l ; i <= r ; ++i)
	{
		if(tmp[i].ty == 1 && tmp[i].num <= mid) update(tmp[i].y , tmp[i].y-tmp[i].x);
		else if(tmp[i].ty == 2 && tmp[i].num > mid) ans[tmp[i].num] = std::min(ans[tmp[i].num] , tmp[i].y-tmp[i].x-query(0,tmp[i].y));
	}
	for(int i = l ; i <= r ; ++i)
		if(tmp[i].ty == 1 && tmp[i].num <= mid) update(tmp[i].y  , -INF);
		

	for(int i = l ; i <= r ; ++i)
	{
		if(tmp[i].ty == 1 && tmp[i].num <= mid) update(tmp[i].y ,  -tmp[i].y-tmp[i].x);
		else if(tmp[i].ty == 2 && tmp[i].num > mid) ans[tmp[i].num] = std::min(ans[tmp[i].num] , -tmp[i].x-tmp[i].y-query(tmp[i].y , mx));
	}
	for(int i = l ; i <= r ; ++i)
		if(tmp[i].ty == 1 && tmp[i].num <= mid)	update(tmp[i].y , -INF);

}
inline int read()
{
	register int x = 0;
	char ch = getchar();
	while(ch > '9' || ch < '0') ch = getchar();
	while(ch <= '9' && ch >= '0') x = (x<<3)+(x<<1) + ch - 48 , ch = getchar();
	return x;
}
int main()
{
	std::memset(ans,0x7f,sizeof(ans));
	n = read() , m = read();
	for(int i = 1 ; i <= n ; ++i){
		q[i].x = read() , q[i].y = read() ,q[i].num = i ,  q[i].ty = 1 , mx = std::max(mx , q[i].x) , mx = std::max(mx , q[i].y);
	}
	for(int i = 1 ; i <= m ; ++i)
		q[n+i].ty = read() , q[n+i].x = read() , q[n+i].y = read() ,q[i+n].num = n+i,  mx = std::max(mx , q[n+i].x) , mx = std::max(mx , q[n+i].y);
	++mx;
	build();
	solve(1,n+m+1);
	for(int i = 1 ; i <= n + m ; ++i)
		if(q[i].ty == 2)
			printf("%d\n",ans[i]);			
	return 0;
}

刚刚又去研究了下zkw线段树，发现比如它维护长度为5的序列，如果你画图会发现这颗线段树每个节点向下不再是中点二分维护区间了，比如上述就是根的左子节点维护1~4，右子节点维护5，但是无论是正确性还是时间复杂度都没有问题，因此对于这种数据结构的研究也就到此为止了。

开始复习点化学到9点。。。