Post 17

Veröffentlicht am | Edited on

不管前方的路有多苦，只要走的方向正确，不管多么崎岖不平，都比站在原地更接近幸福。

可持久化线段树

又名函数式线段树，是重要的数据结构之一。支持静态区间第k小。

主要思想就是能利用现有不变的节点就不开点，每次只会增加

个节点.

为了让BLOG看上去不是那么空，我们找几张图来理解一下

FotileTree

这张图应该很好懂每次插入。

主席树一个经典的运用是区间第k大问题。

显然它的内部结构是不变的，满足可减性。可以用差分来处理（减掉）左端点左边的。

又因为我们是把节点一个一个插进去的，因此对于每个前缀我们都能通过

访问，就可以询问右端点。

现在我们知道如何确定在这个区间查询，然后在这个区间内如何用线段树查询区间第k大呢？

很显然需要使用权值线段树，对于当前区间，我们记录每个值域节点有多少个数！假设查询到节点k，假如k的左节点的值大于k，就继续向左节点递归，否则递归右节点k-cnt。

和Treap是相似的。

还有一个奇怪的地方是离散化相同的值不能给相同的权排名，否则会WA

然后就可以上模板题了。

【模板】可持久化线段树 1（主席树）

题目背景

这是个非常经典的主席树入门题——静态区间第K小

数据已经过加强，请使用主席树。同时请注意常数优化

题目描述

如题，给定N个正整数构成的序列，将对于指定的闭区间查询其区间内的第K小值。

输入输出格式

输入格式：

第一行包含两个正整数N、M，分别表示序列的长度和查询的个数。

第二行包含N个正整数，表示这个序列各项的数字。

接下来M行每行包含三个整数l, r, kl,r,k , 表示查询区间[l, r][l,r]内的第k小值。

输出格式：

输出包含k行，每行1个正整数，依次表示每一次查询的结果

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
5 5
25957 6405 15770 26287 26465 
2 2 1
3 4 1
4 5 1
1 2 2
4 4 1

输出样例#1：

1
2
3
4
5
6405
15770
26287
25957
26287

说明

数据范围：

题解

分析同上。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
// luogu-judger-enable-o2
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <map>
#define maxn 200005
struct Node{
	int v , k;
	bool operator<(const Node& x)const{
		return v < x.v;
	}
}p[maxn];
int v[maxn] , n , m , ct , rev[maxn];
struct FortileTree
{
	int lc[maxn<<5] , rc[maxn<<5] , tot , rt[maxn] , val[maxn<<5];
	int insert(int now , int l , int r , int pos , int vk)
	{
		int p = ++tot;
		lc[p] = lc[now];
		rc[p] = rc[now];
		val[p] = val[now];
		if(l == r){
			val[p] += vk;
			return p;
		}
		int mid = l + r >> 1;
		if(pos <= mid) lc[p] = insert(lc[now] , l , mid , pos , vk);
		else rc[p] = insert(rc[now] , mid + 1 , r , pos , vk);
		val[p] = val[lc[p]] + val[rc[p]];
		return p;
	}
	void build(int &p , int l , int r)
	{
		p = ++tot;
		if(l == r) return;
		int mid = l + r >> 1;
		build(lc[p] , l , mid);
		build(rc[p] , mid + 1 , r);
		val[p] = val[lc[p]] + val[rc[p]];
	}
	int query(int p , int q , int l , int r , int k)
	{
		int mid = l + r >> 1 , cnt = val[lc[q]] - val[lc[p]];
		if(l == r) return l;
		if(k <= cnt) return query(lc[p] , lc[q] , l , mid , k);
		else return query(rc[p] , rc[q] , mid + 1 , r , k - cnt);
	}
}tr;
int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&p[i].v) , p[i].k = i;
	std::sort(p+1,p+n+1);

	for(int i = 1 ; i <= n ; ++i)
		v[p[i].k] = ++ct , rev[ct] = p[i].v;
	tr.build(tr.rt[0] , 1 , ct);
	for(int i = 1 ; i <= n ; ++i)
		tr.rt[i] = tr.insert(tr.rt[i-1] , 1 , ct , v[i] , 1);
	for(int i = 1 ; i <= m ; ++i)
	{
		int x , y , z;
		scanf("%d%d%d",&x,&y,&z);
		if(z > y - x + 1) {puts("0") ; continue;}
		printf("%d\n",rev[tr.query(tr.rt[x-1],tr.rt[y],1,ct,z)]);
	}
}

【模板】可持久化数组

题目背景

UPDATE : 最后一个点时间空间已经放大

标题即题意

有了可持久化数组，便可以实现很多衍生的可持久化功能（例如：可持久化并查集）

题目描述

如题，你需要维护这样的一个长度为 NN 的数组，支持如下几种操作

  1. 在某个历史版本上修改某一个位置上的值
  2. 访问某个历史版本上的某一位置的值

此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
8
9
10
11
12
5 10
59 46 14 87 41
0 2 1
0 1 1 14
0 1 1 57
0 1 1 88
4 2 4
0 2 5
0 2 4
4 2 1
2 2 2
1 1 5 91

输出样例#1：

1
2
3
4
5
6
59
87
41
87
88
46

说明

数据规模：

经测试，正常常数的可持久化数组可以通过，请各位放心

数据略微凶残，请注意常数不要过大

另，此题I/O量较大，如果实在TLE请注意I/O优化

询问生成的版本是指你访问的那个版本的复制

题解

显然这时候就不需要向区间静态第k大一样去建权值线段树了，每次操作我们都新生成一条链，加在主席树上

时间复杂度

，空间复杂度

不过对于此题还是能较轻松通过的。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
// luogu-judger-enable-o2
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 1000005
inline int read()
{
    int x = 0 , f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1 ;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = (x << 3) + (x << 1) + ch - 48;
        ch = getchar();
    }
    return x * f;
}
int n , m , lc[maxn<<5] , rc[maxn<<5] , v[maxn<<5] , tot, root[maxn], p[maxn];
void build(int &node , int l , int r)
{
    node = ++tot;
    if(l == r)
    {
        v[node] = p[l];
        return;
    }
    int mid = l + r >> 1;
    build(lc[node] ,l ,mid);
    build(rc[node] ,mid + 1 , r);
}
int modify(int p , int l , int r , int node , int val)
{
    int np = ++tot;
    lc[np] = lc[node];
    rc[np] = rc[node];
    if(l == r){
        v[np] = val;
        return np;
    }
    int mid = l + r >> 1;
    if(p <= mid)
        lc[np] = modify(p , l , mid , lc[node] , val);
    else rc[np] = modify(p ,  mid + 1 , r , rc[node] , val);
    return np;
}
int query(int p , int l , int r , int pos)
{
    int mid = l + r >> 1;
    if(l == r)	return v[p];
    if(pos <= mid) return query(lc[p] , l , mid , pos);
    else return query(rc[p] , mid + 1 , r , pos);
}
int main()
{
    n = read() , m = read();
    for(int i = 1 ; i <= n ; ++i)
        p[i] = read();
    build(root[0],1,n);
    for(int i = 1 ; i <= m ; ++i)
    {
        int ver , ty, x , y;
        ver = read() , ty = read() , x = read();
        if(ty == 1){
            y = read();
            root[i] = modify(x , 1 , n , root[ver] , y);
        }
        else if(ty == 2){
            root[i] = root[ver];
            printf("%d\n",query(root[ver] , 1 , n , x));
        }
    }
}

【模板】可持久化并查集

题目描述

n个集合 m个操作

操作：

  • 1 a b 合并a,b所在集合
  • 2 k 回到第k次操作之后的状态(查询算作操作)
  • 3 a b 询问a,b是否属于同一集合，是则输出1否则输出0

输入输出格式

输入格式：

输出格式：

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
5 6
1 1 2
3 1 2
2 0
3 1 2
2 1
3 1 2

输出样例#1：

1
2
3
1
0
1

说明

题解

算是个比较重要的数据结构吧。

学习和调试的时间不短，加起来高达3个小时多，其中思考的问题与最后理清的思路就分享下吧。

首先要说一句基本的并查集按秩合并：当两颗树的高度一样的时候合并显然合并后的那个根节点的深度是原来+1，不妨自己画图看看。其他情况的话就是维持高度大的那个。

再一点，要把思路理清楚，显然几个函数的功能明确，共同完成维护可持久化不相交集合。

也就是说平常我们写的并查集只需要把每个点换成在函数式线段树上二分查找就可以了。

详细说说：

初始化建树

1
2
3
4
5
6
7
void build(int &rt,int l,int r)
{
    rt=++cnt;
    if(l==r){fa[rt]=l;return ;}
    build(lson);build(rson);
}
// 就是普通的可持久化数组构建法，不过维护的是Fa而已

trick：传址使得维护父子关系更加方便。

合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void merge(int las , int &now , int l , int r, int pos , int fa)
{
	now = ++ tot;
	lc[now] = lc[las];
	rc[now] = rc[las];
	if(l == r)
	{
		f[now] = fa;
		dep[now] = dep[las];
		return;
	}
	int mid = l + r >> 1;
	if(pos <= mid) merge(lc[las] , lc[now] , l , mid , pos , fa);
	else merge(rc[las] , rc[now] , mid + 1 , r , pos , fa);
}

pos和Fa我们会在主函数中用后面介绍的find函数找到，分别表示两个联通块的根节点。别忘了给dep赋值。

查询某一个值所在可持久化数组中的下标

1
2
3
4
5
6
7
8
int query(int node , int l , int r , int pos)
{
	if(l == r)
		return node;
	int mid = l + r >> 1;
	if(pos <= mid) return query(lc[node] , l , mid , pos);
	else return query(rc[node] , mid + 1 , r , pos);
}

相当于一个数组下标为pos的值，rt是功能需要（通过root进入主席树）。

查找祖先

1
2
3
4
5
6
int find(int x , int p)
{
	int now = query(x , 1 , n , p);
	if(f[now] == p) return now;
	return find(x , f[now]);
}

显然找到当前点在树上的节点然后访问其父亲，和并查集类似，除了访问元素需要二分查找。

这样一来我们就可以上最后跑的挺快的代码了。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 200005
int lc[maxn<<5] , rc[maxn<<5] , dep[maxn<<5] , f[maxn<<5] , n , m , tot , root[maxn];
void build(int &now , int l , int r)
{
    now = ++tot;
    if(l == r){
        f[now] = l;
        return;
    }
    int mid = l + r >> 1;
    build(lc[now] , l , mid);
    build(rc[now] , mid + 1 , r);
    return;
}
void merge(int las , int &now , int l , int r, int pos , int fa)
{
    now = ++ tot;
    lc[now] = lc[las];
    rc[now] = rc[las];
    if(l == r)
    {
        f[now] = fa;
        dep[now] = dep[las];
        return;
    }
    int mid = l + r >> 1;
    if(pos <= mid) merge(lc[las] , lc[now] , l , mid , pos , fa);
    else merge(rc[las] , rc[now] , mid + 1 , r , pos , fa);
}
int query(int node , int l , int r , int pos)
{
    if(l == r)
        return node;
    int mid = l + r >> 1;
    if(pos <= mid) return query(lc[node] , l , mid , pos);
    else return query(rc[node] , mid + 1 , r , pos);
}
int find(int x , int p)
{
    int now = query(x , 1 , n , p);
    if(f[now] == p) return now;
    return find(x , f[now]);
}
int main()
{
    scanf("%d%d",&n,&m);
    build(root[0] , 1 , n);
    for(int i = 1 ; i <= m ; ++i)
    {
        int x , y , op;
        scanf("%d%d",&op,&x);
        if(op == 1)
        {
            root[i] = root[i-1];
            scanf("%d",&y);
            int fx = find(root[i] , x) , fy = find(root[i] , y);
            if(f[fx] != f[fy])
            {
                if(dep[fx] > dep[fy]) std::swap(fx , fy);
                merge(root[i-1] , root[i] , 1 , n , f[fx] , f[fy]);
                if(dep[fx] == dep[fy]) dep[fy] ++ ;
            }
        }
        else if(op == 2) root[i] = root[x];
        else
        {
            root[i] = root[i-1];
            scanf("%d",&y);
            int fx = find(root[i] , x) , fy = find(root[i] , y);
            if(f[fx] != f[fy]) puts("0");
            else puts("1");
        }
    }
}

可持久化Trie

一如既往的可持久化思想，和前面介绍的可持久化线段树很想。

原理简单来说就是对于当前节点u以及上次插入的同深度的节点v，如果它们有共同的边指向父亲（显然某个地方断开了后面也不能再连节点了，Trie定义。假设能连，那就同时让u,v到下一字符c子节点），u需要继承v的所有儿子，除了当前字符c依旧需要新建节点以外，其他点都用v即可。

显然和原来Trie的空间复杂度是一样的，时间复杂度同样都是线性关于插入字符串总长。

举道例题：

最大异或和

题目描述

给定一个非负整数序列\{a\}，初始长度为N。

有M个操作，有以下两种操作类型：

  1. A x：添加操作，表示在序列末尾添加一个数xx，序列的长度N+1。

  2. Q l r x：询问操作，你需要找到一个位置pp，满足

    ，使得：

    最大，输出最大是多少。

输入输出格式

输入格式：

第一行包含两个整数 N,M，含义如问题描述所示。
第二行包含 N个非负整数，表示初始的序列A 。
接下来 M行，每行描述一个操作，格式如题面所述。

输出格式：

假设询问操作有 T 个，则输出应该有 T行，每行一个整数表示询问的答案。

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
5  5
2  6 4 3 6
A 1 
Q 3 5 4 
A 4
Q 5 7 0 
Q 3 6 6

输出样例#1：

1
2
3
4
5
6

说明

题解

一般看到连续的异或区间不难想到前缀异或。因为对于一个连续的区间异或和就是

然后我们相当于对询问快速给出

问题其实转换成给出一个数（24位无符号01串也行）

让你在数组一个范围内找到那个符合条件的数。

复习下用Trie如何贪心找一个数最大异或值：由于从高位开始，所以能反就反，因为后面就算所有位都能反，其和也小于当前一位。

我们能不能用普通的Trie插入然后打上结束标记呢？也不是不行，我们给每个Trie节点一个vector，然后把子节点的下标（读入顺序）合并到vector，然后查询的时候就可以看看和当前位异或的节点的vector里有没有在l~r中的。显然这个复杂度很爆炸，每次查找实际上是

的。

显然使用可持久化我们可以退回r-1那个版本，这样我们只需要找一个最大的了（因为肯定满足小于r），就像线段树一样向上合并最大值就可以了（因为要尽量找到大于等于l-1的与这位相反的数），假设有，那就选择这个节点，没有就走另一边。

显然正确性同上面所述。

这样我们就有了

的算法。

读入优化可通过本题。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cstring>
#define maxn 500005
int p , s[maxn] , tr[maxn<<5][2] , n , tot , root[maxn<<1] , m , mk[maxn<<5];
void insert(int node , int preNode , int k , int len)
{
    if(!~len){
        mk[node] = k;
        return;
    }
    int c = s[k] >> len & 1;
    if(preNode) tr[node][c ^ 1] = tr[preNode][c ^ 1];
    tr[node][c] = ++tot;
    insert(tr[node][c] , tr[preNode][c] , k , len - 1);
    mk[node] = std::max(mk[tr[node][c]] , mk[tr[node][c^1]]);
}
int query(int node , int val , int limit , int len)
{
    if(!~len)	return s[mk[node]] ^ val;//!~!~!~!~!~do not forget ! , !!!
    int c = val >> len & 1;
    if(mk[tr[node][c^1]] >= limit)
        return query(tr[node][c^1] , val , limit , len - 1);
    else return query(tr[node][c] , val , limit , len - 1);
}
int main()
{
    std::memset(mk,-1,sizeof(mk));
    scanf("%d%d",&n,&m);
    for(int i = 1 ; i <= n ; ++i)
        scanf("%d",&p) , s[i] = s[i-1] ^ p;
    root[0] = ++tot;
    insert(root[0] , 0 , 0 , 24);
    for(int i = 1 ; i <= n ; ++i)
        root[i] = ++tot , insert(root[i] , root[i-1] , i , 24);
    for(int i = 1 ; i <= m ; ++i)
    {
        char op;
        scanf("\n%c",&op);
        if(op == 'A')
        {
            int x;
            scanf("%d",&x);
            root[++n] = ++tot;
            s[n] = s[n-1] ^ x;
            insert(root[n] , root[n-1] , n , 24);
        }
        else{
            int x , y , z;
            scanf("%d%d%d",&x,&y,&z);
            z ^= s[n];
            printf("%d\n",query(root[y-1] , z , x-1 , 24));
        }
    }
}

小a和uim之大逃离.

题目背景

小a和uim来到雨林中探险。突然一阵北风吹来，一片乌云从北部天边急涌过来，还伴着一道道闪电，一阵阵雷声。刹那间，狂风大作，乌云布满了天空，紧接着豆大的雨点从天空中打落下来，只见前方出现了一个披头散发、青面獠牙的怪物，低沉着声音说：“呵呵，既然你们来到这，只能活下来一个！”。小a和他的小伙伴都惊呆了！

题目描述

瞬间，地面上出现了一个n*m的巨幅矩阵，矩阵的每个格子上有一坨0~k不等量的魔液。怪物各给了小a和uim一个魔瓶，说道，你们可以从矩阵的任一个格子开始，每次向右或向下走一步，从任一个格子结束。开始时小a用魔瓶吸收地面上的魔液，下一步由uim吸收，如此交替下去，并且要求最后一步必须由uim吸收。魔瓶只有k的容量，也就是说，如果装了k+1那么魔瓶会被清空成零，如果装了k+2就只剩下1，依次类推。怪物还说道，最后谁的魔瓶装的魔液多，谁就能活下来。小a和uim感情深厚，情同手足，怎能忍心让小伙伴离自己而去呢？沉默片刻，小a灵机一动，如果他俩的魔瓶中魔液一样多，不就都能活下来了吗？小a和他的小伙伴都笑呆了！

现在他想知道他们都能活下来有多少种方法。

输入输出格式

输入格式：

第一行，三个空格隔开的整数n，m，k

接下来n行，m列，表示矩阵每一个的魔液量。同一行的数字用空格隔开。

输出格式：

一个整数，表示方法数。由于可能很大，输出对1 000 000 007取余后的结果。

输入输出样例

输入样例#1：

1
2
3
2 2 3
1 1
1 1

输出样例#1：

1
4

说明

【题目来源】

lzn改编

【样例解释】

样例解释：四种方案是：(1,1)->(1,2),(1,1)->(2,1),(1,2)->(2,2),(2,1)->(2,2)。

【数据范围】

对于20%的数据，n,m<=10,k<=2

对于50%的数据，n,m<=100,k<=5

对于100%的数据，n,m<=800,1<=k<=15

题解

很显然的方案数dp

状态肯定是

表示到(i,j)剩余k，是谁取的方案数为多少。

转移就是上一步可能的两个位置，加法原理。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 805
#define maxk 20
#define mod 1000000007
int f[maxn][maxn][maxk][2] , n , m , k , p[maxn][maxn];
int main()
{
	scanf("%d%d%d",&n,&m,&k);
	++k;
	for(int i = 1 ; i <= n ; ++i)
		for(int j = 1 ; j <= m ; ++j)
			scanf("%d",&p[i][j]) , f[i][j][p[i][j]%k][0] = 1;
	for(int i = 1 ; i <= n ; ++i)
		for(int j = 1 ; j <= m ; ++j)
			for(int t = 0 ; t <= k ; ++t)
			{
				(f[i+1][j][(t+p[i+1][j])%k][0] += f[i][j][t][1]) %= mod;
				(f[i][j+1][(t+p[i][j+1])%k][0] += f[i][j][t][1]) %= mod;
				(f[i+1][j][(t-p[i+1][j]+k)%k][1] += f[i][j][t][0]) %= mod;
				(f[i][j+1][(t-p[i][j+1]+k)%k][1] += f[i][j][t][0]) %= mod;
			}
	int ans = 0;
	for(int i = 1 ; i <= n ; ++i)
		for(int j = 1 ; j <= m ; ++j)
			(ans += f[i][j][0][1]) %= mod;
	printf("%d",ans);

}

学习一下Splay吧。。。

虽然不会证复杂度不算学会Splay。。等下次回家看看Splay的复杂度证明。

学习源来自zyf学姐的blog！可能边学边copy过来了。。。

步入正题。

欢迎去学姐blog里学习。

https://blog.csdn.net/clove_unique/article/details/50630280

Splay入门经典

变量声明：

f[i]表示i的父结点，**

表示i的左儿子，

表示i的右儿子 , $key_i$表示i的关键字（即结点i代表的那个数字），$cnt_i$表示$i$结点的关键字出现的次数（相当于权值），$size_i$表示包括i的这个子树的大小；$sz$为整棵树的大小，$root$为整棵树的根。

【clear操作】

将当前点的各项值都清0（用于删除之后）,时间复杂度$O(1)$

1
2
3
inline void clear(int x){
     ch[x][0]=ch[x][1]=f[x]=cnt[x]=key[x]=size[x]=0;
}

【get操作】

判断当前点是它父结点的左儿子还是右儿子，时间复杂度$O(1)$

1
2
3
inline int get(int x){
     return ch[f[x]][1]==x;
}

【update操作】：

更新当前点的size值（用于发生修改之后） ,时间复杂度$O(1)$

1
2
3
4
5
6
7
inline void update(int x){
     if (x){
          size[x]=cnt[x];
          if (ch[x][0]) size[x]+=size[ch[x][0]];
          if (ch[x][1]) size[x]+=size[ch[x][1]];
     }
}

【旋转操作】：

务必完全理解这个操作，这是平衡树最重要的，复杂度得到保证的操作

【rotate操作图文详解】

img

这是原来的树，假设我们现在要将D结点rotate到它的父亲的位置。

  • step 1：

找出D的父亲结点（B）以及父亲的父亲（A）并记录。判断D是B的左结点还是右结点。

  • step 2：

我们知道要将Drotate到B的位置，二叉树的大小关系不变的话，B就要成为D的右结点了没错吧？

咦？可是D已经有右结点了，这样不就冲突了吗？怎么解决这个冲突呢？

我们知道，D原来是B的左结点，那么rotate过后B就一定没有左结点了对吧，那么正好，我们把G接到B的左结点去，并且这样大小关系依然是不变的，就完美的解决了这个冲突。如下图。

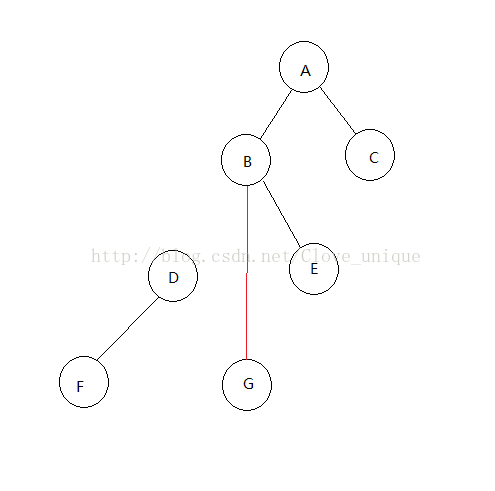
Splay2

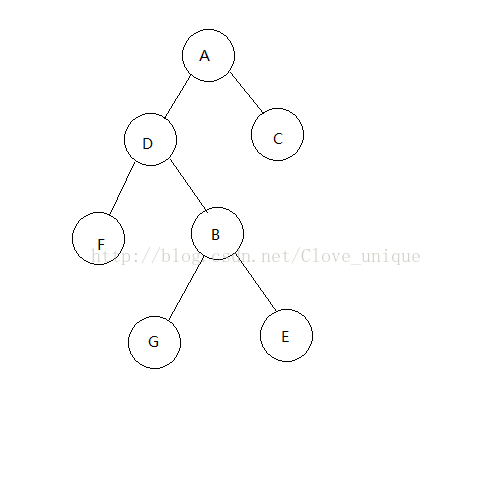
Splay3

这样我们就完成了一次rotate，如果是右儿子的话同理。step 2的具体操作：

我们已经判断了D是B的左儿子还是右儿子，设这个关系为K；将D与K关系相反的儿子的父亲记为B与K关系相同的儿子（这里即为D的右儿子的父亲记为B的左儿子）；将D与K关系相反的儿子的父亲即为B（这里即为把G的父亲记为B）；将B的父亲即为D；将D与K关系相反的儿子记为B（这里即为把D的右儿子记为B）；将D的父亲记为A。

最后要判断，如果A存在（即rotate到的位置不是根的话），要把A的儿子即为D。

显而易见，rotate之后所有牵涉到变化的父子关系都要改变。以上的树需要改变四对父子关系，BG DG BD AB，需要三个操作（BG BD AB）。

  • step 3：update一下当前点和各个父结点的各个值

以前Treap我写旋转都是左旋右旋分开写。。想必看了上面的图不难发现规律并把两个写在一起。

并且不要漏了某些父子关系忘了修改，显然比递归传址维护父子麻烦点。

1
2
3
4
5
6
7
8
9
inline void rotate(int x){
     int old=f[x],oldf=f[old],which=get(x);
     ch[old][which]=ch[x][which^1];f[ch[old][which]]=old;
     f[old]=x;ch[x][which^1]=old;
     f[x]=oldf;
     if (oldf)
          ch[oldf][ch[oldf][1]==old]=x;
     update(old);update(x);
}

接下来是Splay操作，大致和Treap一样但是好像需要分更多情况讨论一下。

【Splay操作】

其实splay只是rotate的发展。伸展操作只是在不停的rotate，一直到达到目标状态。如果有一个确定的目标状态，也可以传两个参。此代码直接splay到根。

splay的过程中需要分类讨论，如果是三点一线的话（x，x的父亲，x的祖父）需要先rotate x的父亲，否则需要先rotate x本身（否则会形成单旋使平衡树失衡）（这东西还需要再去了解一下）

1
2
3
4
5
6
inline void splay(int x){
     for (int fa;(fa=f[x]);rotate(x))
          if (f[fa])
               rotate((get(x)==get(fa)?fa:x));
     root=x;
}

【insert操作】

其实插入操作是比较简单的，和普通的二叉查找树基本一样。

step 1：如果root=0，即树为空的话，做一些特殊的处理，直接返回即可。

step 2：按照二叉查找树的方法一直向下找，其中：

如果遇到一个结点的关键字等于当前要插入的点的话，我们就等于把这个结点加了一个权值。因为在二叉搜索树中是不可能出现两个相同的点的。并且要将当前点和它父亲结点的各项值更新一下。做一下splay。

如果已经到了最底下了，那么就可以直接插入。整个树的大小要+1，新结点的左儿子右儿子（虽然是空）父亲还有各项值要一一对应。并且最后要做一下他父亲的update（做他自己的没有必要）。做一下splay。！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
inline void insert(int v){
     if (root==0) 
     {sz++;ch[sz][0]=ch[sz][1]=f[sz]=0;key[sz]=v;cnt[sz]=1;size[sz]=1;root=sz;return;}
     int now=root,fa=0;
     while (1){
          if (key[now]==v){
               cnt[now]++;update(now);update(fa);splay(now);break;
          }
          fa=now;
          now=ch[now][key[now]<v];
          if (now==0){
               sz++;
               ch[sz][0]=ch[sz][1]=0;key[sz]=v;size[sz]=1;
               cnt[sz]=1;f[sz]=fa;ch[fa][key[fa]<v]=sz;
               update(fa);
               splay(sz);
               break;
          }
     }
}

【find操作】

查询x的排名

初始化：ans=0，当前点=root

和其它二叉搜索树的操作基本一样。但是区别是：

如果x比当前结点小，即应该向左子树寻找，ans不用改变（设想一下，走到整棵树的最左端最底端排名不就是1吗）。

如果x比当前结点大，即应该向右子树寻找，ans需要加上左子树的大小以及根的大小（这里的大小指的是权值）。

不要忘记了再splay一下

1
2
3
4
5
6
7
8
9
10
11
12
13
inline int find(int v){
     int ans=0,now=root;
     while (1){
          if (v<key[now])
               now=ch[now][0];
          else{
               ans+=(ch[now][0]?size[ch[now][0]]:0);
               if (v==key[now]) {splay(now);return ans+1;}
               ans+=cnt[now];
               now=ch[now][1];
          }
     }
}

【findx操作】

找到排名为x的点

初始化：当前点=root

和上面的思路基本相同：

如果当前点有左子树，并且x比左子树的大小小的话，即向左子树寻找；

否则，向右子树寻找：先判断是否有右子树，然后记录右子树的大小以及当前点的大小（都为权值），用于判断是否需要继续向右子树寻找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline int findx(int x){
     int now=root;
     while (1){
          if (ch[now][0]&&x<=size[ch[now][0]])
               now=ch[now][0];
          else{
               int temp=(ch[now][0]?size[ch[now][0]]:0)+cnt[now];
              if (x<=temp){
                  splay(now);
                  return key[now];
              }
               x-=temp;now=ch[now][1];
          }
     }
}

【pre/next操作】

这个操作十分的简单，只需要理解一点：在我们做insert操作之后做了一遍splay。这就意味着我们把x已经splay到根了。求x的前驱其实就是求x的左子树的最右边的一个结点，后继是求x的右子树的左边一个结点（想一想为什么？）

1
2
3
4
5
6
7
8
9
10
11
inline int pre(){
     int now=ch[root][0];
     while (ch[now][1]) now=ch[now][1];
     return now;
}
 
inline int next(){
     int now=ch[root][1];
     while (ch[now][0]) now=ch[now][0];
     return now;
}

【del操作】

删除操作是最后一个稍微有点麻烦的操作。

step 1：随便find一下x。目的是：将x旋转到根。

step 2：那么现在x就是根了。如果cnt[root]>1，即不只有一个x的话，直接-1返回。

step 3：如果root并没有孩子，就说名树上只有一个x而已，直接clear返回。

step 4：如果root只有左儿子或者右儿子，那么直接clear root，然后把唯一的儿子当作根就可以了（f赋0，root赋为唯一的儿子）

剩下的就是它有两个儿子的情况。

step 5：我们找到新根，也就是x的前驱（x左子树最大的一个点），将它旋转到根。然后将原来x的右子树接到新根的右子树上（注意这个操作需要改变父子关系）。这实际上就把x删除了。不要忘了update新根。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
inline void del(int x){
     int whatever=find(x);
     if (cnt[root]>1) {cnt[root]--;update(root);return;}
     //Only One Point
     if (!ch[root][0]&&!ch[root][1]) {clear(root);root=0;return;}
     //Only One Child
     if (!ch[root][0]){
          int oldroot=root;root=ch[root][1];f[root]=0;clear(oldroot);return;
     }
     else if (!ch[root][1]){
          int oldroot=root;root=ch[root][0];f[root]=0;clear(oldroot);return;
     }
     //Two Children
     int leftbig=pre(),oldroot=root;
     splay(leftbig);
     f[ch[oldroot][1]]=root;
     ch[root][1]=ch[oldroot][1];
     clear(oldroot);
     update(root);
     return;
}

区间树明天再学(上面的Treap不都能干嘛。。)