Post 12

Veröffentlicht am | Edited on

I’m going where you are there.

Power收集

题目背景

据说在红雾异变时，博丽灵梦单身前往红魔馆，用十分强硬的手段将事件解决了。

然而当时灵梦在Power达到MAX之前，不具有“上线收点”的能力，所以她想要知道她能收集多少P点，然而这个问题她答不上来，于是她找到了学OI的你。

题目描述

可以把游戏界面理解成一个N行M列的棋盘，有K个格子上有P点，其价值为val(i,j)

初始灵梦可以选择在第一行的任意一个格子出发，每秒她必须下移一格。

灵梦具有一个左右移动的速度T，可以使她每秒向左或右移动至多T格,也可以不移动，并且不能折返。移动可视为瞬间完成，不经过路途上的点，只能获得目标格子的P点。

求最终她能获得的POWER值最大是多少？

输入输出格式

输入格式：

第一行四个数字，N,M,K,T

接下来K行每行3个数字x,y,v,代表第x行第y列有一个val为v的P点，数据保证一个格子上最多只有1个P点。

输出格式：

一个数字

输入输出样例

输入样例#1：

1
2
3
4
5
3 3 4 1
1 1 3
1 2 1
2 2 3
3 3 3

输出样例#1：

1
9

说明

对于40%的测试点，1<=N,M,T,K<=200

对于100%的测试点，1<=N,M,T,K<=4000

v<=100，N,M,K,T均为整数

题解

这种dp已经是最基本的了，再不会就别学了

先随手写个

的dp：设f_{i,j}表示第i行走到位置j的最大利益，然后枚举上一行的合法点转移即可

然后单调队列优化，结果单调队列的判断非空写反了，空的不空，不空是空。。。然后调了半天

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cstring>
#define maxn 4005
int f[maxn][maxn] , n , v[maxn][maxn] , t , k , m , ans;
struct Deque
{
	int que[maxn];
	int l , r;
	Deque(){
		l = 1 , r = 0;
		std::memset(que,0,sizeof(que));
	}
	inline void clear(){
		l = 1 , r = 0;
		std::memset(que,0,sizeof(que));
	}
	inline void pop_front(){
		que[l++] = 0;
	}
	inline void pop_back(){
		que[r--] = 0;
	}
	inline void push_back(int x){
		que[++r] = x;
	}
	inline int front(){
		return que[l];
	}
	inline int back(){
		return que[r];
	}
	inline int size(){
		return r - l + 1;
	}
	inline void print()
	{
		puts("THE ELES :");
		for(int i = l ; i <= r ; ++i)
			printf("%d ",que[i]);
		putchar(10);
	}
}q;
int main()
{
	scanf("%d%d%d%d",&n,&m,&k,&t);
	for(int i = 1 ; i <= k ; ++i){
		int x ,y , val;
		scanf("%d%d%d",&x,&y,&val);
		v[x][y] = val;
	}
	for(int i = 1 ; i <= n ; ++i)
	{
		int now = 1;
		for(int j = 1 ; j <= m ; ++j)
		{
			while(now <= j + t && now <= m){
				while(q.size() && f[i-1][q.back()] < f[i-1][now]) q.pop_back();
				q.push_back(now);
				++now;
			}
			while(q.size() && q.front() < j - t) q.pop_front();
		    f[i][j] = f[i-1][q.front()] + v[i][j];
			ans = std::max(ans , f[i][j]);
		}
		q.clear();
	}
	printf("%d",ans);
}

[POI2007]EGZ-Driving Exam

题目描述

The Byteotian driving licence exam takes place in an area in which there are nn straight, parallel, unidirectional, north-oriented streets (that is the allowed driving direction is south to north). Each of the streets is exactly mm meters long, all of them begin and end on the same level. These streets are numbered from 11 to nn starting the westernmost. There are also pp unidirectional, east or west-oriented streets perpendicular to the abovementioned, each one of them connecting a pair of adjacent north-oriented streets. It is also possible that an east-oriented and a west-oriented street overlap, thus forming a bidirectional one.

img

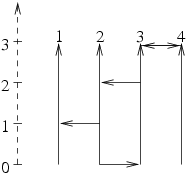
An exemplary testing area (n=4, m=3, p=5n=4,m=3,p=5).

The examiner chooses a north-oriented street, at the beginnig of which the examination starts and anothernorth-oriented street, where it is to come to an end. The task of the applicant is to drive from the starting tothe final point, observing the allowed directions.The examiner always chooses as starting point a street, from which it is possible to drive to the endpointof any other north-oriented street.The work of the examiners is a very tedious one, because they always have to start at the beginning ofone of the few suitable streets. The board of directors have decided to build a new testing area on the basis ofpre-existent plans. It has been calculated, that available funds allow for no more than kk east or west-orientedstreets to be built. Those new streets are to be constructed in such a way, so as to add the largest possiblenumber of potential starting points (there may or may not exist starting points on the pre-existent plan). Newstreets have to connect pairs of adjacent north-oriented streets.

Task

Write a programme which:

  • reads a description of the testing area and the number kk from the standard input,
  • calculates the greatest number of potential new starting points for the examination, generated by adding no more than kk east or west-oriented streets,
  • writes the outcome to the standard output.

成都的驾驶考试在一个有n条平行的自南向北的单向的道路的场地中进行。每条道路长度为m米，并且都在同一条水平线上开始和结束。街道从西向东分别编号为1到n。同样有p条单向的自西向东或自东向西的街道垂直于上面描述的街道，每一条这样的街道链接了两个相邻的自南向北的道路。当然自西向东和自东向西的道路可以重叠，那就是一个双向的街道了。

考生选择一个自南向北的道路作为他考试的起始点和另外一个自南向北的道路作为他考试的终止点。他们的考试项目是将车从开始的道路驾驶到作为终止点的道路。考生们总是选择一个可以到达所有其他街道的起始道路作为开始点。现在，考生们总是感到十分无趣因为他们只有很少的起始道路可以选择，所以教练们决定改造先有的考试场所，由于经费的限制，他们决定添加至多K条东西向的道路，使得能够选择的起始道路尽量地多。

输入输出格式

输入格式：

In the first line of the standard input there are four integers nn, mm, pp and kk (2 \le n \le 100\ 0002≤n≤100 000, 1 \le m, k, \le 100\ 0001≤m,k,≤100 000, 0 \le p \le 100\ 0000≤p≤100 000), separated by single spaces, denoting respectively: the number of north-oriented streets, the length of each one of them, the number of pre-existent east or west-oriented streets, the maximal number of new streets to be built. The north-oriented streets are numbered from 11 to nn, starting with the westernmost.

The following pp lines contain three integers each: n_ini, m_imi and d_idi (1 \le n_i \le n1≤ni≤n, 0 \le m_i \le m0≤mi≤m, d_i \in \{0, 1\}di∈{0,1}), separated by single spaces, denoting the ‘th east-oriented (for d_i=0di=0) or west-oriented (for d_i=1di=1) street. This street connects north-oriented streets nn and n+1n+1, intersecting them in points m_imi meters distant from their beginning.

输出格式：

The first and only line of the standard output should contain a single integer, denoting the maximal numberof new examination starting points generated by building no more than kk east or west-oriented streets. Thenewly built streets do not have to intersect the north-oriented streets in points, whose distance from thebeginning of the street is an integer. The newly built east or west-oriented streets may overlap, thus formingbidirectional streets.

输入输出样例

输入样例#1：

1
2
3
4
5
6
4 3 5 2
2 0 0
2 2 1
3 3 1
1 1 1
3 3 0

输出样例#1：

1
2

题解

这道题实际上是道最长单调子序列啊。。

首先不难想到答案一定是一个连续的区间去掉本来就能到达任意点的点数。

考虑最长单调子序列的性质：在权重相同的情况下用最小的改变代价使得整个序列单调。

这个性质很好证明，反证法即可，假如有另一个序列使得剩下的（剩下的必定每个都要调整，因为不然就可以加进当前的子序列）用更少的步数单调，那这个就比最长单调子序列长了。

假如看不懂上面的论述，可以自己用反证法想想。

有这个性质后，我们可以预处理出每个点到左边最少需要建的路，到右边需要建的路。

预处理出这个后，发现这两个相加的和满足某种单调性。具体来说，我们可以选取一段区间，使得左端点能到最右边，右端点能到最左边，这个区间里的点除掉那些一开始就满足条件的就是当前答案。

取最大即可。

没有写Code

[SCOI2009]粉刷匠

题目描述

windy有 N 条木板需要被粉刷。 每条木板被分为 M 个格子。 每个格子要被刷成红色或蓝色。

windy每次粉刷，只能选择一条木板上一段连续的格子，然后涂上一种颜色。 每个格子最多只能被粉刷一次。

如果windy只能粉刷 T 次，他最多能正确粉刷多少格子？

一个格子如果未被粉刷或者被粉刷错颜色，就算错误粉刷。

输入输出格式

输入格式：

第一行包含三个整数，N M T。

接下来有N行，每行一个长度为M的字符串，’0’表示红色，’1’表示蓝色。

输出格式：

包含一个整数，最多能正确粉刷的格子数。

输入输出样例

输入样例#1：

1
2
3
4
3 6 3
111111
000000
001100

输出样例#1：

1
16

说明

30%的数据，满足 1 <= N,M <= 10 ； 0 <= T <= 100 。

100%的数据，满足 1 <= N,M <= 50 ； 0 <= T <= 2500 。

题解

一道对我来说好难好难的dp啊，mhr学长觉得我连这种题都不会，联赛分数肯定上不了350QAQ。（真实

%mhr学长秒切，稳进省队。

首先由于每块木板之间不能连续刷，一个很自然的子问题之一就是木板数。

然后我们也许可以知道对于一块木板前i个格子刷了k次能粉刷的最多格子数，然后就可以愉快的泛化物品用分组背包解决。

然后这种比较麻烦的预处理我一向是不会写的，其实不是个很难的划分dp。

设

表示当前木板前$i$个格子粉刷$j$次，涂0/1颜色的最大粉刷格子数。

枚举当前位置，枚举最后粉刷的一段的左端点，然后很自然想到枚举已经刷的次数，显然和上一段有很简单的递推关系。假如和上一段颜色相同，相当于从上一段接着刷的，假如不同，说明需要多用一次。然后加上当前枚举的颜色这一段的个数。

然后这个预处理复杂度小于背包过程复杂度，因此时间复杂度为

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cstring>
#define maxn 55
#define maxT 2505
#define ll long long
int g[maxn][maxn][2] , f[maxT] , n , m , t , ct[2][maxn];
char s[maxn][maxn];
int main()
{
	scanf("%d%d%d",&n,&m,&t);
	for(int i = 1 ; i <= n ; ++i)
	{
		scanf("%s",s[i]+1);
		char *now = s[i];
		std::memset(ct,0,sizeof(ct));
		for(int j = 1 ; j <= m ; ++j)
			ct[now[j]-48][j] = ct[now[j]-48][j-1] + 1 , ct[(now[j]-48)^1][j] = ct[(now[j]-48)^1][j-1];
		for(int j = 1 ; j <= m ; ++j)
			for(int k = 1 ; k <= j ; ++k)
				for(int l = 1 ; l <= m ; ++l)
					for(int x = 0 ; x < 2 ; ++x)
						g[j][l][x] = std::max(g[k-1][l][x] , g[k-1][l-1][x^1]) + ct[x][j] - ct[x][k-1];
		for(int j = t ; ~j ; --j)
			for(int k = 1 ; k <= j && k <= m ; ++k)
				for(int p = 1 ; p <= m ; ++p)
					f[j] = std::max(f[j] , f[j-k] + std::max(g[p][k][0],g[p][k][1]));
	}
	int ans = 0;
	for(int i = 1; i <= t ; ++i)
		ans = std::max(ans , f[i]);
	printf("%d",ans);
}

[USACO17JAN]Promotion Counting晋升者计数

题目描述

The cows have once again tried to form a startup company, failing to remember from past experience that cows make terrible managers!

The cows, conveniently numbered 1 \ldots N1…N (1 \leq N \leq 100,0001≤N≤100,000), organize the company as a tree, with cow 1 as the president (the root of the tree). Each cow except the president has a single manager (its “parent” in the tree). Each cow ii has a distinct proficiency rating, p(i)p(i), which describes how good she is at her job. If cow ii is an ancestor (e.g., a manager of a manager of a manager) of cow jj, then we say jj is a subordinate of ii.

Unfortunately, the cows find that it is often the case that a manager has less proficiency than several of her subordinates, in which case the manager should consider promoting some of her subordinates. Your task is to help the cows figure out when this is happening. For each cow ii in the company, please count the number of subordinates jj where p(j) > p(i)p(j)>p(i).

奶牛们又一次试图创建一家创业公司，还是没有从过去的经验中吸取教训—牛是可怕的管理者！

为了方便，把奶牛从 1 \cdots N(1 \leq N \leq 100, 000)1⋯N(1≤N≤100,000) 编号，把公司组织成一棵树，1 号奶牛作为总裁（这棵树的根节点）。除了总裁以外的每头奶牛都有一个单独的上司（它在树上的 “双亲结点”）。所有的第 ii 头牛都有一个不同的能力指数 p(i)p(i)，描述了她对其工作的擅长程度。如果奶牛 ii 是奶牛 jj 的祖先节点（例如，上司的上司的上司），那么我们我们把奶牛 jj 叫做 ii 的下属。

不幸地是，奶牛们发现经常发生一个上司比她的一些下属能力低的情况，在这种情况下，上司应当考虑晋升她的一些下属。你的任务是帮助奶牛弄清楚这是什么时候发生的。简而言之，对于公司的中的每一头奶牛 ii，请计算其下属 jj 的数量满足 p(j) > p(i)p(j)>p(i)。

输入输出格式

输入格式：

The first line of input contains NN.

The next NN lines of input contain the proficiency ratings p(1) \ldots p(N)p(1)…p(N) for the cows. Each is a distinct integer in the range 1 \ldots 1,000,000,0001…1,000,000,000.

The next N-1N−1 lines describe the manager (parent) for cows 2 \ldots N2…N. Recall that cow 1 has no manager, being the president.

输入的第一行包括一个整数 NN。

接下来的 NN 行包括奶牛们的能力指数

. 保证所有数互不相同，在区间

之间。

接下来的 N-1 行描述了奶牛

的上司（双亲节点）的编号。再次提醒，1 号奶牛作为总裁，没有上司。

输出格式：

Please print N lines of output. The ith line of output should tell the number of subordinates of cow i with higher proficiency than cow i.

输出包括 NN 行。输出的第 ii 行应当给出有多少奶牛 ii 的下属比奶牛 ii 能力高。

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
8
9
10
5
804289384
846930887
681692778
714636916
957747794
1
1
2
3

输出样例#1：

1
2
3
4
5
2
0
1
0
0

题解

一道挺水的题。

显然求子树中大于它的可以离散化后用权值树状数组解决。只需要按深度优先的顺序让每个点的子树全都在它前插入即可，注意去除兄弟子树的影响，解决方法是记录下当前的数量。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 100005
int head[maxn] , cnt, bit[maxn] , f[maxn] , g[maxn] , n , v[maxn] , tot , sz[maxn];
struct edge{
	int next , to;
}e[maxn<<1];
struct Node{
	int v , k;
	bool operator<(const Node& x)const{
		return v < x.v;
	}
}p[maxn];
inline int query(int x){
	int ans = 0;
	for(int i = x ; i ; i -= i & -i)
		ans += bit[i];
	return ans;
}
inline void update(int x , int v){
	for(int i = x ; i <= tot ; i += i & -i)
		bit[i] += v;
}
inline void add(int x, int y)
{
	e[++cnt].next = head[x];
	e[cnt].to = y;
	head[x] = cnt;
}
void pre(int x , int fx)
{
	sz[x] = 1;
	for(int i = head[x] ; i ; i = e[i].next)
		if(e[i].to != fx)
			pre(e[i].to , x) ,sz[x] += sz[e[i].to];
}
void DFS(int x , int fx)
{
	g[x] = query(v[x]);
	for(int i = head[x] ; i ; i = e[i].next)
	{
		int v = e[i].to;
		if(v == fx) continue;
		DFS(v , x);
	}
	//printf("%d %d %d %d\n",x,sz[x],query(v[x]),g[x]);
	f[x] = sz[x] - 1 - (query(v[x]) - g[x]);
	update(v[x] , 1);
}
int main()
{
	scanf("%d",&n);
	for(int i = 1; i <= n ; ++i)
		scanf("%d",&p[i].v) , p[i].k = i;
	for(int i = 2 ; i <= n ; ++i){
		int x;
		scanf("%d",&x);
		add(i , x) , add(x , i);
	}
	std::sort(p+1,p+n+1);
	p[0].v = 425727;
	tot = 1;
	for(int i =1 ; i <= n ; ++i)
	{
		if(p[i].v == p[i-1].v)
			v[p[i].k] = tot;
		else v[p[i].k] = ++tot;
	}
	pre(1,1);
	DFS(1,1);
	for(int i = 1;  i <= n ; ++i)
		printf("%d\n",f[i]);
}

1638 - Pole Arrangement

题目描述

小 Z 是一个很有名的建筑师，有一天他接到了一个很奇怪的任务：在数轴上建 nn 个建筑，每个建筑的高度是 11到 nn 之间的一个整数。

小 Z 有很严重的强迫症，他不喜欢有两个建筑的高度相同。另外小 Z 觉得如果从最左边（所有建筑都在右边）看能看到 AA 个建筑，从最右边（所有建筑都在左边）看能看到 BB 个建筑，这样的建筑群有着独特的美感。现在，小 Z 想知道满足上述所有条件的建筑方案有多少种？

如果建筑 ii 的左(右)边没有任何建造比它高，则建筑 ii 可以从左(右)边看到。两种方案不同，当且仅当存在某个建筑在两种方案下的高度不同。

输入输出格式

输入格式：

第一行一个整数 TT，代表 TT 组数据。 接下来 TT 行，每行三个整数 n,A,Bn,A,B。

输出格式：

对于每组数据输出一行答案

输入输出样例

输入样例#1：

1
2
3
2
3 2 2
3 1 2

输出样例#1：

1
2
2
1

题解

作为建筑师的弱化版，我们只需要一个

的算法。

显然设

表示前$i$个数，从左边能看到$j$个，从右边能看到$k$个。

我们发现正着插进去算方案数不是很好算，我们考虑把最矮的插进去。（非常巧妙了qwq）

然后像普通的组合递推一样用加法原理合并状态就好了。（分三种情况，插在最左边，插在最右边，插在中间）

比较经典和基础的一道递推，学习了。。。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cstring>
#define maxn 125
#define ll long long
#define mod 1000000007
ll f[maxn][maxn][maxn] , n , l , r;
ll DFS(int k , int ls , int rs)
{
	if(~f[k][ls][rs]) return f[k][ls][rs];
	if(k == 1 && ls == 1 && rs == 1)	return f[k][ls][rs] = 1;
	else if(k <= 1) return f[k][ls][rs] = 0;
	return f[k][ls][rs] = DFS(k-1 , ls - 1 , rs) % mod + DFS(k-1 , ls , rs - 1) % mod + 1ll* (k - 2) * DFS(k - 1 , ls , rs) % mod;
}
int main()
{
	std::memset(f,-1,sizeof(f));
	int t;
	scanf("%d",&t);
	while(~(--t) && scanf("%d%d%d",&n,&l,&r))
		std::cout << DFS(n , l , r) % mod << std::endl;
}

使用Vim想要编译需要记住的命令

1
w<cr>: ! g++ %:r.cpp -o %:r.exe -g -Wall -DDebug<cr>: ! %:r.exe<cr>