树状数组学习笔记

Veröffentlicht am | Edited on

准备加强一下树状数组的使用？

首先来看一维区间修改+查询怎么做。

还是要应用差分。

思路还是很简单的。。

放代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <algorithm>
#define maxn 1000005
#define lowbit(x) x & (-x)
long long BIT[3][maxn] , c[maxn] , n , t[maxn] , m , op , l , r , v;
inline void update(int,int,int);
inline long long query(int,int);//first is the query type
inline void init();
int main()
{
    freopen("6.in","r",stdin);
    freopen("my.out","w",stdout);
    scanf("%lld%lld",&n,&m);
    for(int i = 1 ; i <= n ; ++i)
        scanf("%lld",&t[i]);
    for(int i = 1 ; i <= n ; ++i)
        c[i] = t[i] - t[i-1];
    // for(int i = 1 ; i <= n ; ++i)
    //     printf("%d\n",c[i]);
    init();
    for(int i = 1 ; i <= m ; ++i)
    {
        scanf("%lld",&op);
        if(op == 1)
        {
            scanf("%lld%lld%lld",&l,&r,&v);
            update(1,l,v) , update(1,r+1,-v);
            update(2,l,v) , update(2,r+1,-v);
        }
        if(op == 2)
        {
            scanf("%lld%lld",&l,&r);
            // printf("%lld %lld %lld %lld\n",(r+1)*query(1,r),query(2,r),l*query(1,l-1),query(2,l-1));
            printf("%lld\n",(r+1)*query(1,r) - query(2,r) - l*query(1,l-1) + query(2,l-1));
        }
    }
}
inline void init()
{
    for(int i = 1 ; i <= n ; ++i)
        update(1,i,c[i]) , update(2,i,c[i]);
        // BIT[1][i] += c[i] , BIT[2][i] += c[i]*i;//why this WA??
        // if(i + lowbit(i) <= n)
        //     BIT[1][i+lowbit(i)] += c[i] , BIT[2][i+lowbit(i)] += c[i]*i;
}
inline long long query(int type , int k)
{
    long long ans = 0;
    if(type == 1)
        for(int i = k ; i ; i -= lowbit(i))
            ans += BIT[1][i];
    else
        for(int i = k ; i ; i -= lowbit(i))
            ans += BIT[2][i];
    return ans;
}
inline void update(int type , int k , int v)
{
    if(type == 1)
        for(int i = k ; i <= n ; i += lowbit(i))
            BIT[1][i] += v;
    else
        for(int i = k ; i <= n ; i += lowbit(i))
            BIT[2][i] += 1ll*v*k;// love vk~
}

2–d树状数组支持维护区间修改区间查询。

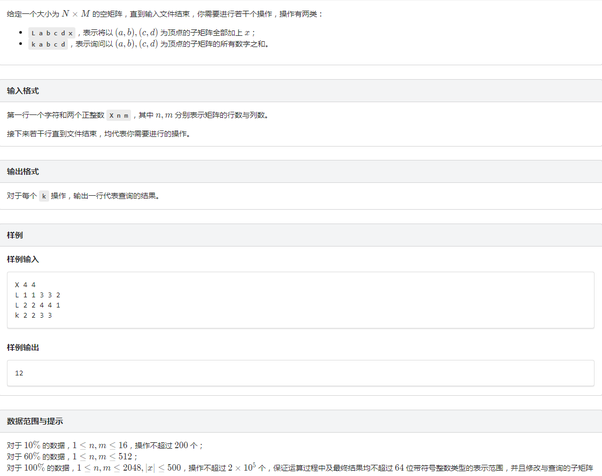
main-qimg-e4c1d97cdbeb0d649b385836c4ba4946.png

显然二维线段树会被卡空间（事实是不会） ， 我们来看看如何用二维树状数组来维护。

img

img

img

AC代码（巨大无比的常数令我很无奈。。最后加了register和快读连同inline才一起过的。。）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// luogu-judger-enable-o2
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <algorithm>
#define lowbit(x) (x) & -(x)
#define maxn 2050
#define re register
int BIT[4][maxn][maxn] , n , m , x , y , a , b , v;
char c;
inline int read()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while(ch > '9' || ch < '0') {
		if(ch == '-') f= -1;
		ch = getchar();
	}
	while(ch <= '9' && ch >= '0')
		x = (x<<3) + (x<<1) + ch - 48 , ch = getchar();
	return x*f;
}
inline int query(int tr , int x , int y)
{
	int ans = 0;
	for(re int i = x ; i ; i -= lowbit(i))
		for(re int j = y ; j ; j -= lowbit(j))
			ans += BIT[tr][i][j];
	return ans;
}
inline int rangeSum(int x, int y)
{
	return query(0,x,y)*(x+1)*(y+1) - query(1,x,y)*(y+1) - query(2,x,y)*(x+1) + query(3,x,y);
}
inline void update(int x , int y , int v)
{
		for(re int i = x ; i <= n ; i += lowbit(i))
			for(re int j = y ; j <= m ; j += lowbit(j))
				BIT[0][i][j] += v , BIT[1][i][j] += v*x  , BIT[2][i][j] += v*y , BIT[3][i][j] += v*x*y;
}
int main()
{
	std::cin>>c;
	scanf("%d%d",&n,&m);
	while(std::cin>>c)
	{
		if(c == 'L')//update 
		{
			a = read() , b = read() , x = read() , y = read() , v = read();
			update(a,b,v) , update(a,y+1,-v), update(x+1,b,-v) , update(x+1,y+1,v);
		}
		else if(c == 'k')
		{
			a = read() , b = read() , x = read() , y = read() ;
			printf("%d\n",rangeSum(x,y)-rangeSum(x,b-1)-rangeSum(a-1,y)+rangeSum(a-1,b-1));
			
		}
	}
}
/*
X 4 4
L 1 1 3 3 2
L 2 2 4 4 1
k 2 2 3 3
*/

友情提示：2-d BIT从上面会发现如果数据比较大是会很容易爆掉的，开long long都么有用，所以二维线段树在空间允许的情况下比较好用。